句法(Syntax)就是研究自然语言中不同成分组成句子的方式以及支配句子结构并决定句子是否成立的规则。
1. 句法结构
两种句法结构:
- Constituency (成分语法)
- Dependency (依存语法)
1.1 成分语法
定义:句法范畴之间具有层次关系,可以形成一颗语法树来表示,用 上下文无关文法(CFGs) 来描述。
Heads、Arguments、Adjuncts
- Heads(中心词): 每一个短语都有一个核心词,这个词决定了整个短语的句法性质。例如:NP:the man -> Head 是man; VP: eat sushi -> Head 是 eat
- Arguments(论元):论元是强制性(Obligatory) 的成分。中心语(Head)“要求”必须有这些成分才能表达完整的意思。论元的数量是固定的。例如:及物动词必须要有宾语。
- Adjuncts(修饰语/附加词):修饰语是可选(Optional) 的成分。它们为句子提供额外的信息(时间、地点、方式等),去掉后句子在语法上依然成立,可以省略也可以重复叠加。
成分语法的缺点:成分语法局限于表层结构分析,不能彻底解决句法和语义问题,因此存在非连续成分、结构歧义等问题。
1.2 依存语法
定义:句法结构不是由短语(如 NP, VP)层层嵌套组成的,而是由单词和单词之间的二元关系(Binary Relations)组成的,结构表现为连接词与词之间的有向弧(Arrows)。
依存语法的核心特点
A. 结构单位:基于单词 (Word-based)
- 与成分语法不同,依存语法中没有短语节点(如 NP, VP)。
- 句子中的每一个成分都对应句法结构中的唯一一个节点(即单词本身)。
B. 关系性质:二元非对称 (Binary & Asymmetric)
- 二元性: 关系只发生在两个单词之间。
- 非对称性: 两个词的地位不平等,一个是中心语,一个是从属语。
- 方向性: 关系是有方向的。通常认为关系从中心语(Head) 指向 依存成分(Dependent)。
C. 角色定义
- 中心成分(Head): 也称为支配者(Governor)或核心词(Regent)。它是关系的起点,决定了句法性质。
- 依存成分(Dependent): 也称为修饰词(Modifier)或从属者(Subordinate)。它是依附于中心语存在的。
D. 关系类型(Typed Dependencies)
- 连线(Arrows)通常带有标签,表示语法关系(如主语
nsubj,宾语dobj等)。 - 这些关系可以细分为不同的层级(如 Carroll 定义了 20 种,Marneffe 定义了 48 种)。
配价理论 (Valency Theory)
配价(Valency),这是决定依存关系建立的依据:
- 定义: “价”是词语的一个属性,表示某个词语与其他词语结合的能力(类似于化学元素的化合价)。
- 配价模式: 描述了一个词在特定语境下,需要哪些词(语义角色)来填补其空缺。这解释了为什么动词(如 eat)能支配名词(如 sushi)。
投射性 (Projectivity)
- 投射性(Projectivity): 如果依存弧线在单词上方绘制时互不交叉,则该结构是投射的。
- 非投射性(Non-Projectivity): 如果弧线发生交叉(通常出现在长距离依赖或自由语序语言中),则为非投射的。
2. 句法分析
Gammar Vs. Parsing
- 文法是“陈述性”的,例如CFGs(上下文无关文法),它们只是定义了什么是合法的句子,只是静态的规则集合
- 句法分析是“过程性”的,动态地用文法规则去执行操作。
句法分析的本质是“搜索”
- 类比:搜索FSA(有限状态自动机)
- 核心:搜索CFG
- 在所有的可能句法结构中,找到最可能正确的句法树
- 搜索空间由文法规则定义
2.1 成分句法分析
2.1.1 Top-Down Parsing
这是一种“目标驱动”的搜索策略,其核心思想是:先假设句子是合法的(即由根节点 S 生成),然后尝试推导出一棵树,看其叶子节点是否能完美匹配输入的单词序列。
1. 核心定义与逻辑
- 方向: 从根节点 $S$(Start Symbol)开始,向下构建,直到叶子节点(Leaves)。
- 规则匹配: 寻找左侧(LHS, Left Hand Side)匹配当前非终结符的文法规则进行展开。
- 例如:当前节点是 $S$,就去文法里找 $S \rightarrow \dots$ 的规则。
- 构建过程: 将规则左侧的符号替换为右侧的符号序列,不断重复,直到生成词性标记(POS)和单词。
2. 具体的搜索策略
光有方向是不够的,因为文法通常有歧义(一个 $S$ 可能对应多条规则),所以需要一种搜索策略。课件中详细描述的是 深度优先、从左到右(Depth-First, Left-to-Right) 的策略。
A. 搜索算法要素
- 深度优先搜索 (DFS): 一条路走到黑。每次只扩展最近生成的那个状态(Tree),如果走不通了,就回溯(Backtrack)。
- Agenda(议程/栈) 用来存储当前搜索的状态。如果当前路径失败,就从 Agenda 中弹出一个旧的状态重试。
- 扩展顺序:
- 节点: 总是优先扩展最左边还没展开的非终结符(Leftmost non-terminal)。
- 规则: 按照文法中定义的顺序依次尝试。
B. 算法流程
- 初始化: 将仅包含根节点 $S$ 的树放入 Agenda,指针指向输入句子的第一个单词。
- 循环: 直到解析成功或 Agenda 为空。
- 取出当前状态
cur。 - 找到
cur中最左边的未扩展节点。 - 如果是词性 (POS): 检查它是否匹配当前输入的单词?
- 匹配: 保留这个树,继续处理下一个节点。
- 不匹配: 这条路死了,丢弃(Backtrack)。
- 如果是短语 (如 NP, VP): 应用文法规则展开它,生成新的树,压入 Agenda。
- 取出当前状态

3. 优缺点分析
Top-Down Parsing 有着非常鲜明的特性,课件第 55 页对其进行了批判性的总结。
✅ 优点 (Pros)
- 绝不产生非法结构: 因为它是从根节点 $S$ 开始构建的,所以它生成的每一棵树(即使是局部的)在语法上都是合法的,都一定是一个 $S$。它不会像 Bottom-Up 那样构建出一堆最后拼不成 $S$ 的孤立碎片。
❌ 缺点 (Cons)
- 浪费时间在“幻觉”上: 它经常会在还没有看输入单词的情况下,就构建出一大堆树。
- 比如:无论输入是什么,它总是先猜句子是 $NP$ 开头的。即使你的输入是 “Does…” (动词开头),它也要先把 $NP \rightarrow Det\ N$ 等所有名词开头的规则试一遍,发现错了才回头。
- “Wastes time on trees that can never match the input.”(在永远无法匹配输入的树上浪费时间)。
- 左递归问题(Left Recursion): Top-Down 解析器通常无法处理 $A \rightarrow A\ B$ 这样的左递归规则(会导致无限循环)。
2.1.2 Bottom-up Parsing
如果说 Top-Down 是一个“理想主义者”(先画蓝图再造楼),那么 Bottom-Up Parsing(自底向上句法分析) 就是一个**“务实派”**。
1. 核心定义与逻辑
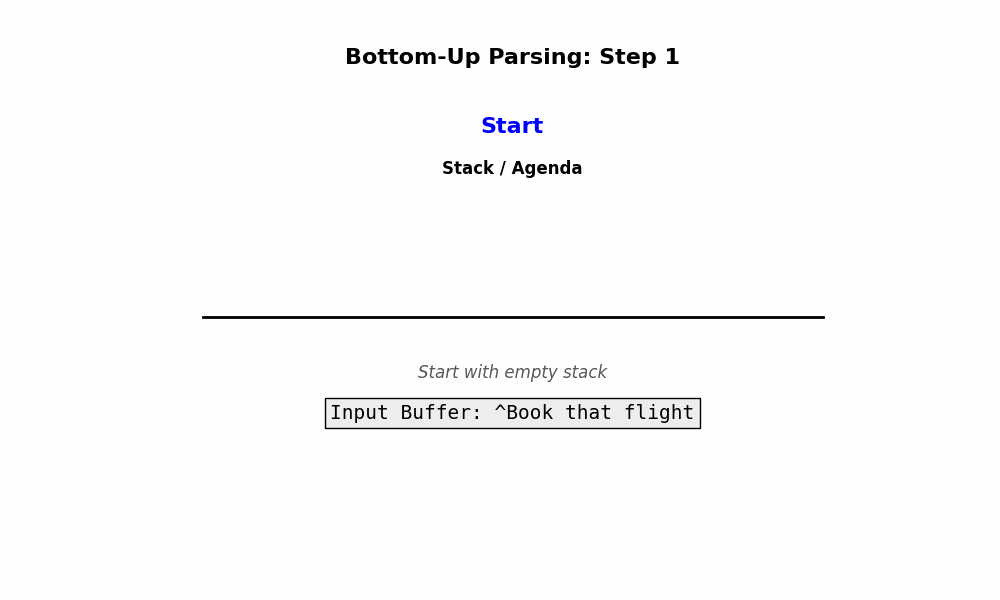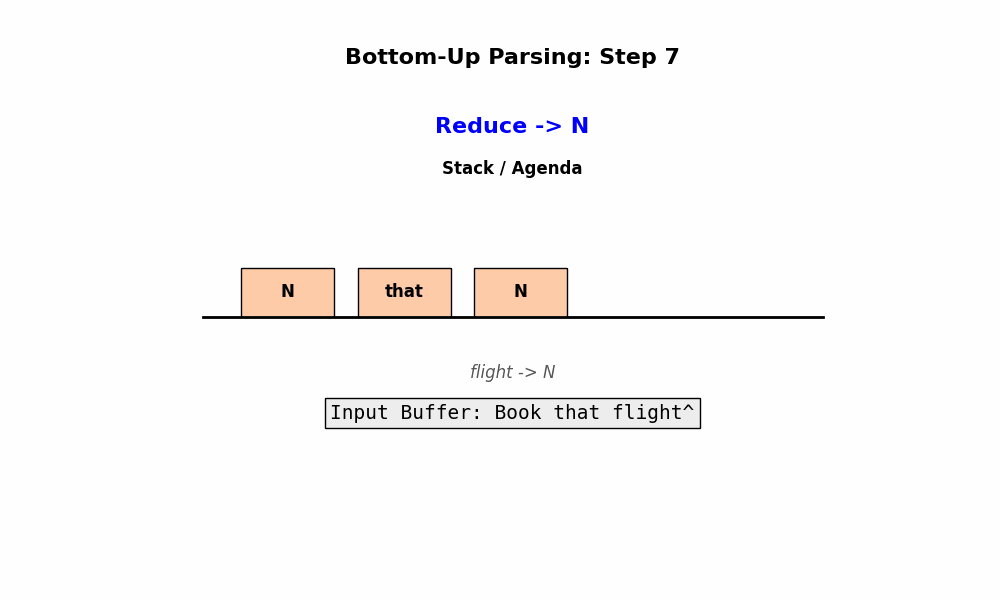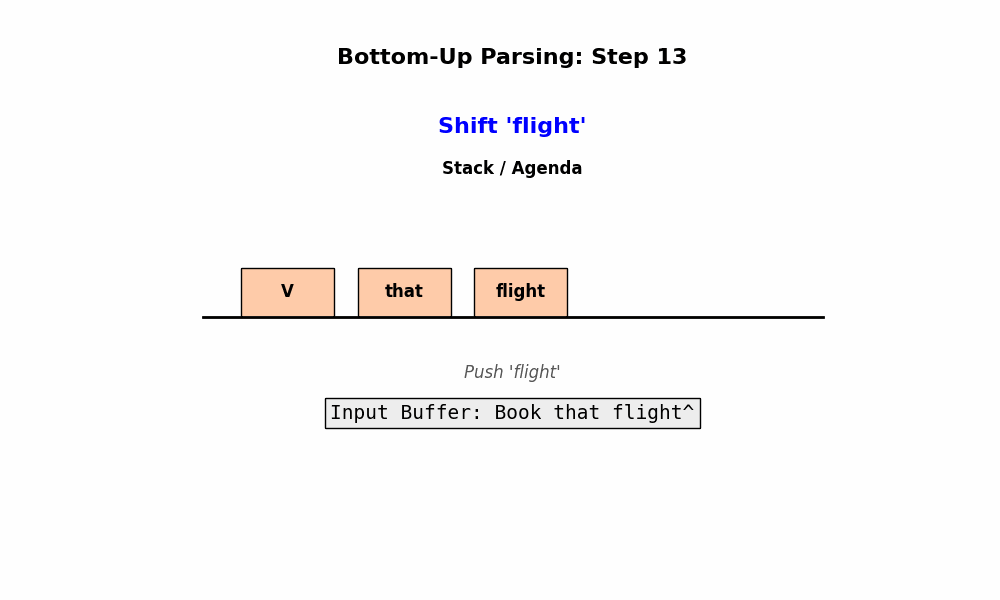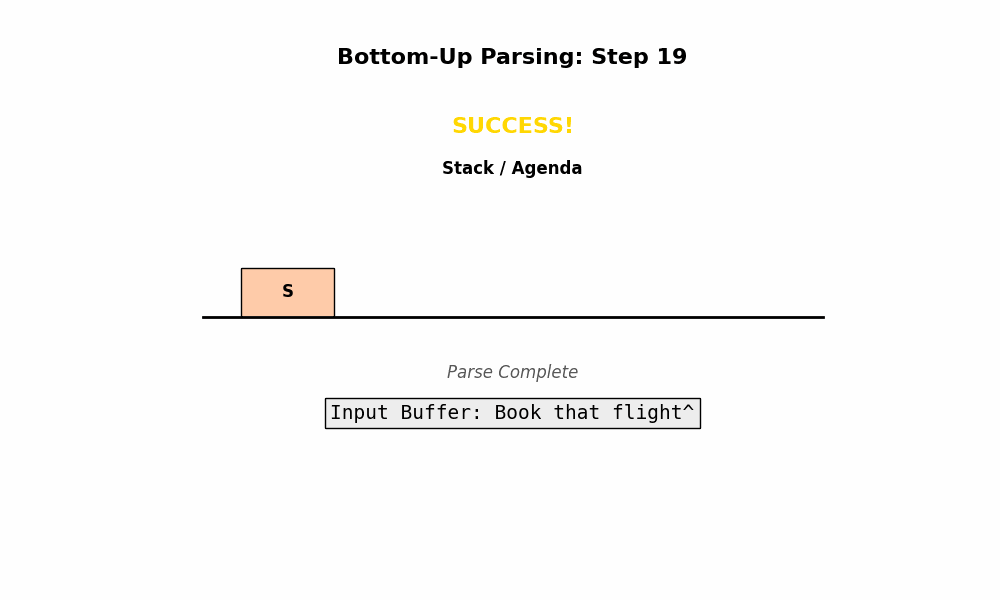
Bottom-Up Parsing 的核心思想是:从输入的单词开始,像搭积木一样,一步步将单词组合成短语,再将短语组合成更大的短语,直到最后拼成一个根节点 $S$。
- 起点: 输入的单词序列(Input words)。
- 动作: 寻找规则的右侧 (Right Hand Side, RHS)。
- 如果当前缓冲区里的序列匹配了某条规则的右边(例如发现了
Det和Noun),就将它们替换为规则左边(LHS)的非终结符(例如NP)。这个过程通常被称为 “Reduce”(归约)。
- 如果当前缓冲区里的序列匹配了某条规则的右边(例如发现了
- 终点: 当整个序列被归约成唯一的起始符号 $S$ 时,分析成功。
2. 具体的搜索策略
基于 深度优先搜索 (Depth-first search) 的 Bottom-Up 策略:
- 初始化: 解析状态(State)就是输入的单词序列。
- 匹配与替换:
- 在当前状态中,寻找与文法规则右侧(RHS)匹配的片段。
- 用规则左侧(LHS)替换该片段。
- 扩展空间 (Agenda): 使用 Agenda 来存储不同的归约路径(因为一个词可能有多种词性,或者一个序列可能有多种组合方式)。
- 成功判定: 当状态中只剩下一个 $S$,且没有多余单词时,解析成功。
3. 优缺点分析
✅ 优点 (Pros)
- 脚踏实地,不产生幻觉:
- 它绝不探索与输入不一致的树。
- Top-Down 可能会在那儿瞎猜“这里有个 NP”,结果输入根本不是。Bottom-Up 只有在看到了
Det和Noun之后,才会建立NP。它构建的每一个子树都是真实存在于句子里的。
❌ 缺点 (Cons)
- 做无用功 (Wastes time on illegal parses):
- 它虽然不产生“幻觉”,但它会生产很多垃圾(无法构成句子的碎片)。
- 比如在 “Book that flight” 的例子中,如果它先把 Book 分析成了名词(Noun),它可能会构建一个名词短语 [NP The Book]。这个短语本身是合法的,但是它在这个句子的语境下是无法向上合并成 $S$ 的。
- “Wastes time exploring illegal parses (no S root).”(在探索无法到达 S 根节点的非法解析上浪费时间)。
2.1.3 Top-Down Vs. Bottom-up
Top-Down Vs. Bottom-up
| 特性 | Top-Down (理想派) | Bottom-Up (务实派) |
|---|---|---|
| 起点 | 根节点 $S$ | 输入单词 |
| 搜索驱动 | 文法规则驱动 (Goal-driven) | 输入数据驱动 (Data-driven) |
| 核心操作 | 展开 (Expand LHS $\to$ RHS) | 归约 (Reduce RHS $\to$ LHS) |
| 主要优点 | 保证最终是一棵树 ($S$) | 保证子树一定匹配单词 |
| 主要缺点 | 容易瞎猜,脱离实际单词 | 容易造出拼不成句子的碎片 |
1. 自顶向下分析器 (Top-Down Parsers)
这种方法试图从语法的起始符号(通常标记为 S,代表 Sentence)开始,通过不断应用语法规则展开,直到匹配输入的单词。
优点(图片中提到的):
它永远不会探索非法的句法结构(never explore illegal parses)。因为它总是从合法的根节点
S开始构建,所以生成的任何子树在语法结构上肯定都是合法的。缺点(What’s wrong):
浪费时间在无法匹配输入的树上(waste time on trees that can never match the input)。
解释:由于它是从抽象的语法规则出发,它可能会生成成千上万种合法的句子结构,但在花了很久生成后,才发现最底层的单词跟用户实际输入的句子根本对不上。这就像在做无用功。
2. 自底向上分析器 (Bottom-Up Parsers)
这种方法从实际输入的单词开始,试图将单词逐步组合成短语,最后向上归约成起始符号 S。
优点(图片中提到的):
它永远不会探索与输入不一致的树(never explore trees inconsistent with input)。因为它直接基于你输入的单词进行构建,所有的子树都确实存在于你的句子中。
缺点(What’s wrong):
浪费时间探索非法的解析(waste time exploring illegal parses)。
解释:它可能会把几个词成功组合成一个短语(比如名词短语),但最后发现这个短语根本没法和其他部分拼在一起形成一个完整的句子(无法到达根节点
S)。就像拼图时拼好了一小块,结果发现这一块根本不属于这幅画。
3. 对于两者的共同问题:控制策略 (Control Strategy)
无论是自顶向下还是自底向上,都需要在庞大的搜索空间中寻找正确的解析路径。幻灯片列出了几个关键的决策问题:
如何探索搜索空间? (How explore search space?)
- 这是指搜索算法的选择。
并行还是回溯? (Pursuing all parses in parallel or backtrack…?)
- 是同时尝试所有可能的路径(并行,耗费内存),还是一条路走到黑,不通再回来选另一条(回溯,耗费时间)?
下一步应用哪条规则? (Which rule to apply next?)
- 当有多个语法规则都适用时,该选哪一个?
下一步扩展哪个节点? (Which node to expand next?)
- 是先处理左边的短语还是右边的短语?
2.1.4 CKY Parsing
我们讨论了 Top-Down(盲目搜索、效率低)和 Bottom-Up(产生大量垃圾碎片、效率低)的局限性。
CKY 算法 (Cocke-Younger-Kasami Algorithm) 的出现,就是为了解决这些问题。它利用动态规划 (Dynamic Programming) 的思想,将句法分析的效率从指数级降低到了多项式级别($O(n^3)$)。
1. 核心思想:分而治之与记忆化
CKY 的核心逻辑是:任何一个长的短语(或句子),都可以拆分成两个较短的相邻短语。
- 动态规划 (Dynamic Programming): 我们将中间结果(短语的分析结果)存这就叫在一个表格(Table/Chart)中。当我们构建更长的短语时,直接查表重用这些结果,而不是重新计算。
- 自底向上 (Bottom-Up): 我们先识别单词,再识别长度为 2 的短语,再识别长度为 3 的……直到长度为 $n$ 的整个句子。
2. 前置条件:乔姆斯基范式 (CNF)
这是 CKY 算法能够运行的绝对前提。标准 CFG 的规则太随意(如 $VP \to V\ NP\ PP$),不便分割。CKY 要求文法必须转化为 Chomsky Normal Form (CNF)。
CNF 的规则只有两种形式:
- $A \rightarrow B\ C$ (两个非终结符)
- $A \rightarrow w$ (一个终结符/单词)
为什么?
这样保证了生成的句法树是二叉树。对于任何一个非叶子节点,它一定是由左右两个子节点合并而来的。这让我们可以用简单的二分法来寻找分割点。
3. 数据结构:三角矩阵 (The Chart)
我们使用一个 $(n+1) \times (n+1)$ 的矩阵来存储中间结果。
- 索引定义: 输入句子被索引分割:$0 \text{ Word}_1\ 1 \text{ Word}_2\ 2 \dots n$。
- 单元格 $table[i, j]$: 存储包含了从位置 $i$ 到 $j$ 的这个片段(Span)所能构成的所有非终结符集合。
4. 算法流程与推导
这是算法的灵魂部分。假设句子长度为 $n$。
第一步:初始化(填对角线)
处理长度为 1 的片段(即单词本身)。
对于句子中的第 $j$ 个单词(位置 $j-1$ 到 $j$):
- 查找规则 $A \rightarrow word_j$。
- 将 $A$ 填入 $table[j-1, j]$。
第二步:填上半三角(核心循环)
我们需要计算长度从 2 到 $n$ 的所有片段。
对于每一个片段 $[i, j]$(起始 $i$,结束 $j$),我们需要寻找一个分割点 $k$ ($i < k < j$),把它切成两半:$[i, k]$ 和 $[k, j]$。
推导公式:
如果在文法中存在规则 $A \rightarrow B\ C$,并且:
- $B$ 存在于 $table[i, k]$ 中(左半边存在)
- $C$ 存在于 $table[k, j]$ 中(右半边存在)
则: 将 $A$ 加入到 $table[i, j]$ 中。
5. 实例演示
让我们看课件中的 “Book the flight through Houston” 例子,或者练习题 “I eat sushi with chopsticks with you”。
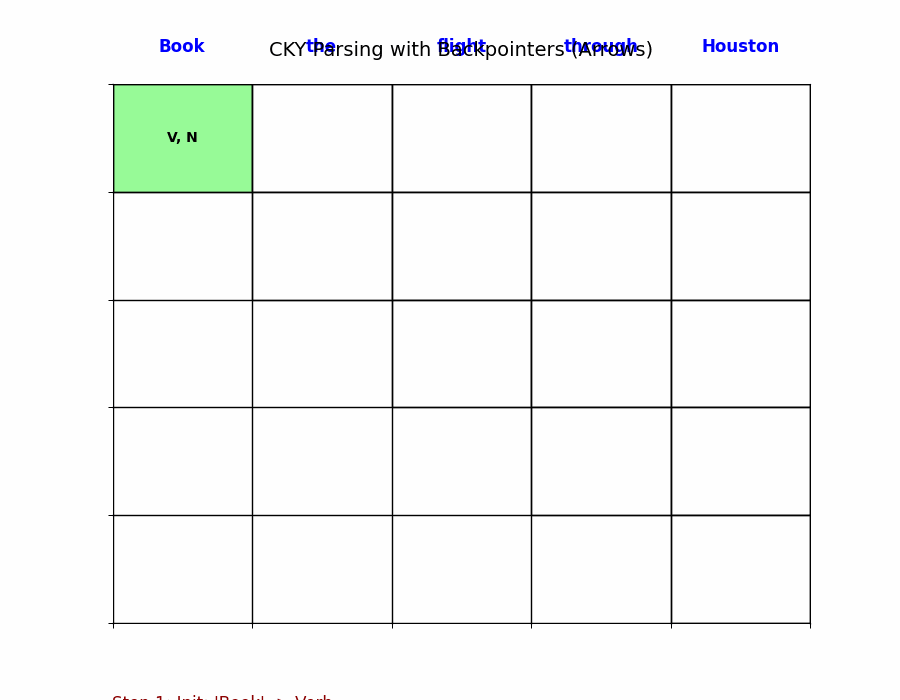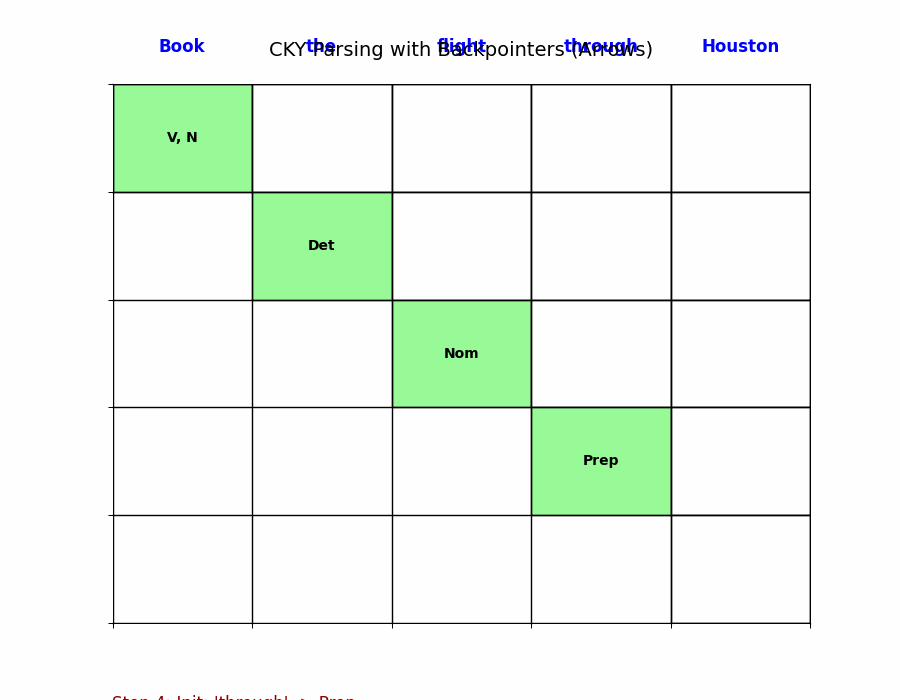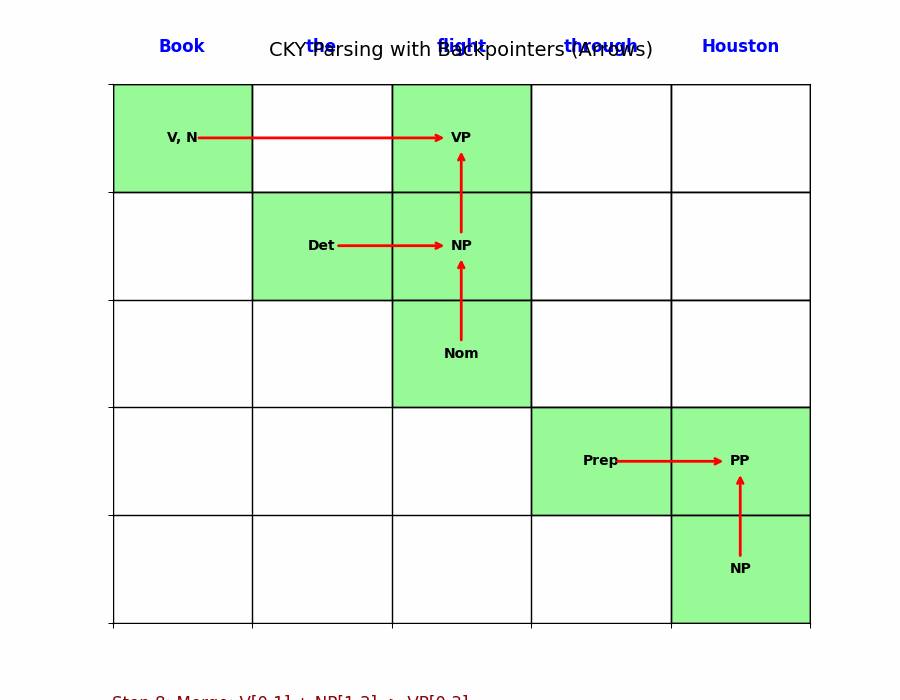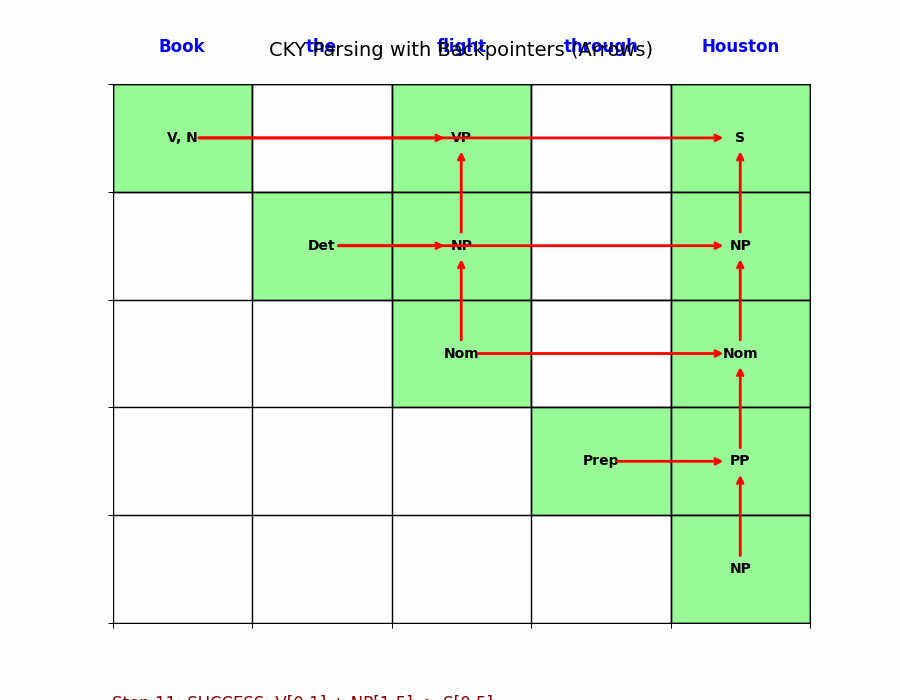
以 $VP \rightarrow Verb\ NP$ 为例,假设我们要填某个高层单元格:
- 算法会在中间切一刀(分割点 $k$)。
- 它查左边的格子 $[i, k]$,发现里面有个 Verb。
- 它查右边的格子 $[k, j]$,发现里面有个 NP。
- 因为它查到了文法规则 $VP \rightarrow Verb\ NP$,所以它在当前格子 $[i, j]$ 填入 VP。
6. 进阶:概率 CKY (Probabilistic CKY)
2.1.5
这是现代 NLP(特别是统计句法分析)真正使用的方法。我们不仅要填“有什么”,还要计算“概率最大的是哪个”。
变化点:
单元格 $table[i, j]$ 不再只存一个集合,而是存储非终结符及其对应的最大概率。
核心推导公式 (Page 98):
对于规则 $A \rightarrow B\ C$,在位置 $[i, j]$ 处,由分割点 $k$ 产生的概率为:
$$P(A_{i,j}) = P(A \rightarrow B\ C) \times P(B_{i,k}) \times P(C_{k,j})$$
算法逻辑:
- 遍历所有可能的分割点 $k$。
- 遍历所有可能的规则 $A \rightarrow B\ C$。
- 计算上述乘积。
- Max 操作: 如果有多种方式能生成 $A$,只保留概率最大的那个,并记录下是指向哪两个子节点(Backpointer,用于回溯构建树)。
CKY 算法之所以伟大,是因为它把一个指数级的搜索问题变成了一个填表游戏:
- 输入: 句子 + CNF 文法。
- 过程:
- 先填底层(单词)。
- 再填上一层(两两组合)。
- 一层层向上,直到右上角的格子 $[0, n]$ 出现 $S$。
- 复杂度: $O(n^3)$。这使得长句子的分析成为可能。
它不仅解决了 Bottom-Up 产生无效碎片的问题(因为它只保留符合规则的组合),也解决了重复计算的问题。
2.1.5 数据统计方法
传统的方法随之文法规则的增加,会产生几百万中解析结果,但是无法确定哪一种才是人类真正想要表达的意思
1. 数据的崛起:Penn Treebank (宾州树库)
为了解决上述问题,NLP 领域引入了大规模的标注数据。其中最著名的是 Penn Treebank (PTB)(Marcus et al., 1993)。
什么是树库?
它不再是一堆抽象的规则,而是成千上万个已经被人类专家标注好句法树的真实句子。- 例子:
((S (NP-SBJ (DT The) (NN move)) (VP (VBD followed) ...)))
- 例子:
树库的价值 (Page 79):
起初,人们觉得建立树库比写文法慢且没用。但事实证明,树库提供了:- 可重用性: 大家都用同一套数据训练。
- 广泛的覆盖面: 覆盖了真实语料中的各种现象。
- 频率和分布信息: 这是统计分析的基础(比如知道“eat”后面接“sushi”的概率比接“idea”大)。
- 评估标准: 提供了一个“金标准”来评判谁的 Parser 更好。
2. 解决方案:统计句法分析 (Statistical Parsing)
核心思想:
有了数据(Treebank),我们就可以统计概率。于是诞生了 PCFG(概率上下文无关文法)。
- 从“是非”到“概率”:
- 以前:这个结构合法吗?(Yes/No)
- 现在:这个结构合法的概率是多少?(Probability)
- 消歧机制:
面对那“数百万种”可能的解析树,统计 Parser 可以计算每一棵树的联合概率,然后挑出概率最高的那一棵(Most Likely Derivation)。
3. 实际应用
引入统计方法后,Parser 的鲁棒性(Robustness)大大增强,终于可以应用于实际的 NLP 任务了:
- 高精度问答系统 (QA)
- 命名实体识别 (NER)
- 机器翻译 (MT)
- 信息抽取 (Information Extraction)
2.1.6 PCKY 算法
如果说标准的 CKY 算法解决了“能不能解析”的问题,那么 Probabilistic CKY (PCKY,概率 CKY 算法) 则解决了**“哪一个是最好的解析”**这个问题。它是现代统计句法分析器的基石。
1. 核心目标与背景 (Why PCKY?)
- 背景: 标准 CKY 只能告诉我们一个句子有哪些可能的树结构。对于有歧义的句子(如 “Book the flight through Houston”),它可能生成多棵树。
- 目标: 在所有可能的句法树中,找到**概率最大(Most Likely)**的那一棵。
- 类比: 这就像是 HMM 模型中的 Viterbi 算法。我们要找的是一条“最可能的路径”。
2. 输入与预处理
算法开始前,必须有两个输入:
- 句子: 待分析的单词序列 $w_1, \dots, w_n$。
- PCFG 文法: 必须是 乔姆斯基范式 (CNF)。
- 规则必须是 $A \rightarrow B\ C$ 或 $A \rightarrow w$。
- 关键点: 每条规则都带有一个概率 $P(Rule)$。
- 注意: 如果原始文法不是 CNF,转化时必须小心计算概率,以保持概率的一致性(Page 99 展示了转化的例子)。
3. 数据结构的变化
在标准 CKY 中,单元格 table[i, j] 里面存的是一个集合(例如 {NP, VP})。
而在 PCKY 中,单元格 table[i, j] 里的每一个非终结符,都要绑定一个最大概率值。
- 结构:
table[i, j][A]= 非终结符 $A$ 覆盖片段 $[i, j]$ 的最大概率。 - 辅助结构(Backpointers): 为了最后能画出树,我们还需要记录这个最大概率是从哪里来的(即:是从哪个分割点 $k$ 和哪两个子节点合并来的)。
4. 算法核心逻辑
PCKY 的运行过程依然是填满 $(n+1) \times (n+1)$ 的三角矩阵,但填表的公式变了。
A. 初始化(底层)
对于句子中的第 $j$ 个单词(位置 $j-1$ 到 $j$):
- 查找所有规则 $A \rightarrow w_j$。
- 填表:
table[j-1, j][A] = P(A -> w_j)。
B. 递归填表(核心公式)
我们要计算非终结符 $A$ 在位置 $[i, j]$ 的概率。
我们需要遍历所有可能的分割点 $k$ ($i < k < j$) 和所有可能的规则 $A \rightarrow B\ C$。
概率计算公式:
$$P(A_{i,j}) = P(A \rightarrow B\ C) \times P(B_{i,k}) \times P(C_{k,j})$$
这里有三项相乘:
- 规则概率: 使用该条文法规则的概率。
- 左子树概率: 左边部分 $[i, k]$ 被解析为 $B$ 的概率(查表得)。
- 右子树概率: 右边部分 $[k, j]$ 被解析为 $C$ 的概率(查表得)。
C. 最大化 (Max) 与 记录 (Argmax)
如果在同一个格子 $[i, j]$,通过不同的分割点 $k$ 或不同的规则都能生成 $A$,我们只保留概率最大的那个。
$$table[i, j][A] = \max_{k, B, C} (P(A \rightarrow B\ C) \times table[i, k][B] \times table[k, j][C])$$
同时,记录下让概率最大的 $k, B, C$,用于回溯。
5. 实例推导:Book the flight
- 规则示例:
- $S \rightarrow VP\ (0.1)$
- $VP \rightarrow Verb\ NP\ (0.5)$
- $Verb \rightarrow Book\ (0.5)$
Step 1: 填单词 (Page 100)
- 单词 “Book” (位置 0-1):
- 查词典:$Verb \rightarrow Book$ (0.5), $S \rightarrow Book$ (0.01)。
- 填入格子
[0, 1]:Verb: 0.5,S: 0.01。
Step 2: 填高层 (Page 106-109)
- 假设我们已经算好了:
[0, 1](Book) 有Verb: 0.5[1, 5](the flight through Houston) 有NP: 0.054(假设值)
- 现在要填
[0, 5](Book…Houston) 的 VP。 - 应用规则 $VP \rightarrow Verb\ NP$ (概率 0.5):
$$P(VP_{0,5}) = 0.5 (\text{规则}) \times 0.5 (\text{Verb}) \times 0.054 (\text{NP}) = 0.0135$$ - 填入格子
[0, 5]:VP: 0.0135。
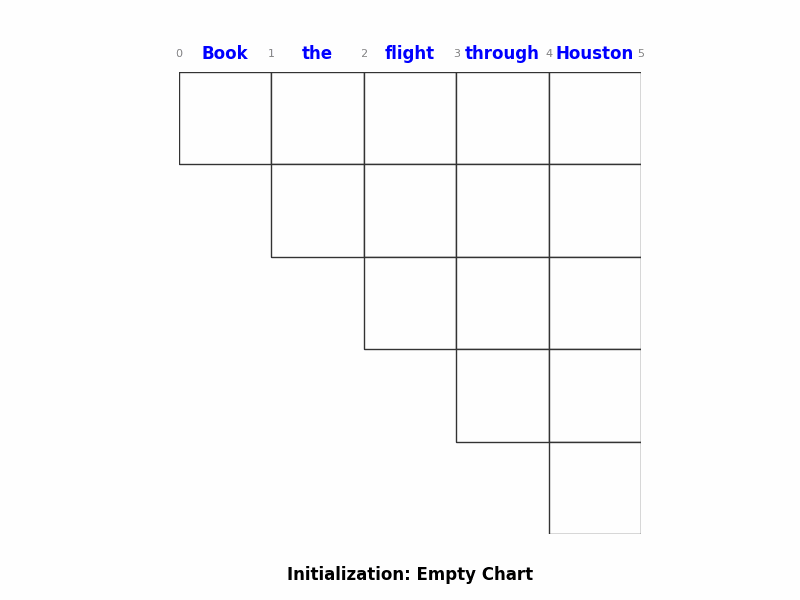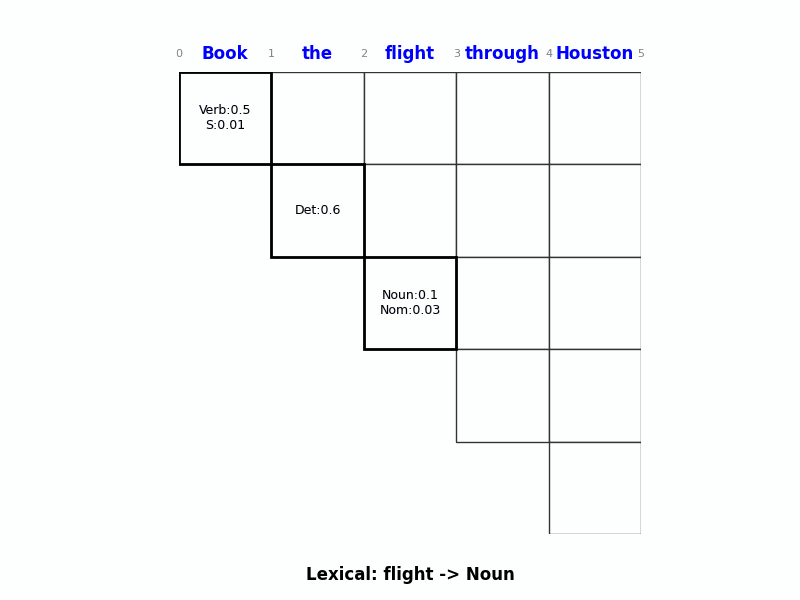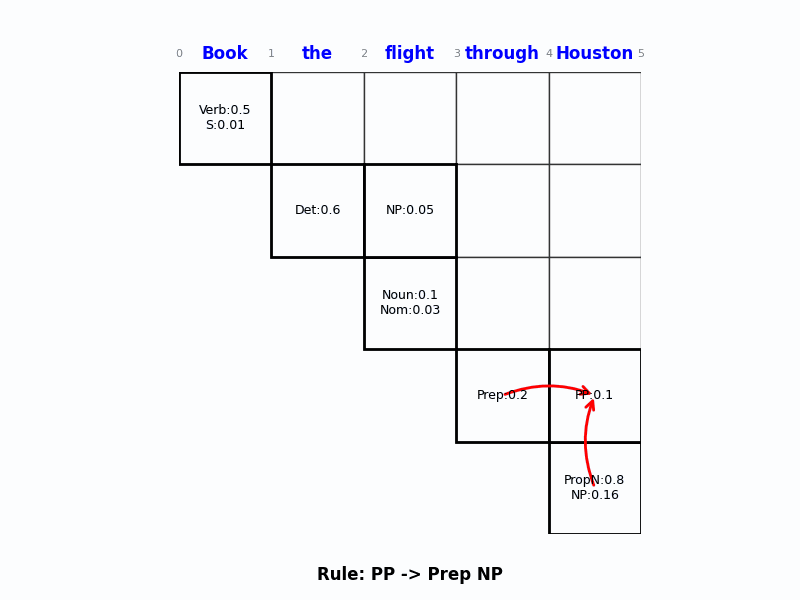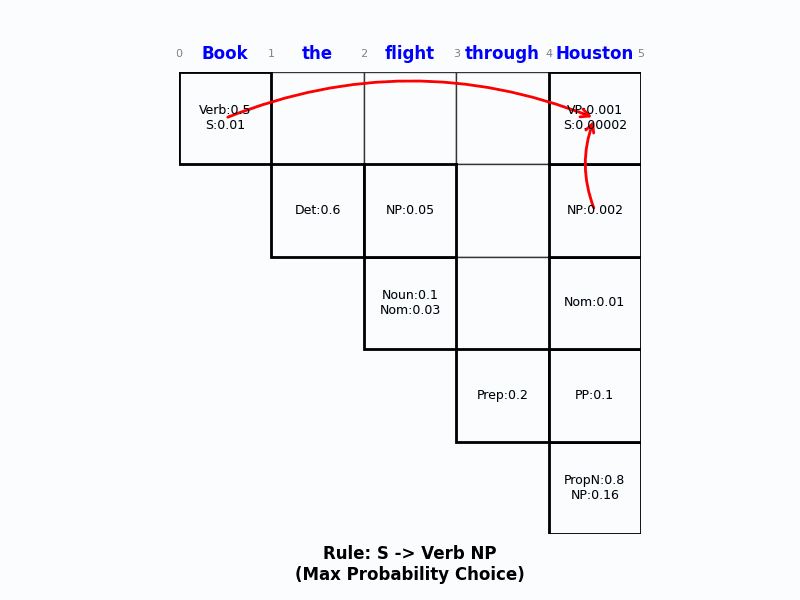
Step 3: 最终决策 (Page 109)
- 到了最右上角的格子
[0, n],可能会得到多个 $S$ 的概率(来自不同的切分方式)。 - 比如:
- 解析 1 的 $S$ 概率:0.0000216
- 解析 2 的 $S$ 概率:0.0000015
- PCKY 算法选择: 0.0000216 对应的解析树作为最终结果。
2.2 PCFG
所谓“训练 PCFG”,通过数学语言描述就是:给定一个 CFG 文法结构 $G$,我们要确定其中每一条规则 $\alpha \rightarrow \beta$ 的概率 $P$,使得该文法能最好地解释手中的数据。
1. 有监督训练 (Supervised Training)
这是最理想也是最常用的情况。
- 前提条件: 我们不仅有句子,还有对应的正确句法树。也就是我们拥有一个 Treebank(树库),比如 Penn Treebank。
- **核心思想:既然答案(句法树)都摆在面前了,我们只需要数数(Counting)**就可以了。这被称为 最大似然估计 (MLE)。
具体做法与公式:
对于任何一条规则,比如 $VP \rightarrow V\ NP$,它的概率计算公式为:
$$P(VP \rightarrow V\ NP | VP) = \frac{\text{Count}(VP \rightarrow V\ NP)}{\text{Count}(VP)}$$
通俗解释:
- 分母: 去树库里数一下,非终结符 $VP$ 一共出现了多少次?(比如 1000 次)。
- 分子: 在这 1000 次 $VP$ 中,有多少次是扩展成了 $V\ NP$ 这种形式的?(比如 600 次)。
- 计算: 概率 = $600 / 1000 = 0.6$。
注意:实际操作中通常还需要进行 平滑 (Smoothing) 处理,以防止某些在训练集中没出现的规则概率变成 0。
2. 无监督训练 (Unsupervised Training)
这是比较困难的情况,通常用于科学研究或缺乏标注数据的场景。
- 前提条件: 我们只有一堆原始句子(Unannotated data),没有对应的句法树。但是我们知道文法的规则集合(比如知道有 $S \rightarrow NP\ VP$ 这条规则,但不知道它的概率)。
- 核心目标: 找到一组概率参数,使得这组参数生成的这些句子的总概率(Likelihood)最大。
核心算法:Inside-Outside Algorithm
这是 EM 算法 (Expectation-Maximization) 在 PCFG 上的具体应用,它与 HMM 中的 Baum-Welch 算法 非常相似。
算法逻辑:
这是一个“鸡生蛋,蛋生鸡”的迭代过程:
- 2.3 初始化 (Initialization): 随机给每一条文法规则分配一个概率。
- E 步 (Expectation / Inside-Outside):
- 用当前的概率去解析手中的句子(使用 Inside 和 Outside 算法计算)。
- 虽然我们不知道真实的树是哪棵,但我们可以计算期望值:在当前概率下,规则 $A \rightarrow B\ C$ 在解析这些句子时预计被用到了多少次?
- M 步 (Maximization):
- 根据 E 步算出来的“期望次数”,重新计算规则的概率(类似于有监督里的数数,只不过数的是“期望”)。
- 迭代: 重复 E 步和 M 步,直到概率收敛(不再变化)。
- 2.4 Inside 算法 (Page 111-114): 用于计算一个子树的生成概率(自底向上)。
- Outside 算法: 用于计算从根节点到该子树外部环境的概率(自顶向下)。两者结合才能算出某条规则在某个位置被使用的期望次数。
局限性
“Experimental results are not impressive”(实验结果并不惊艳)。
- 因为 PCFG 的非凸性,EM 算法很容易陷入局部最优解。
- 如果没有额外的约束,无监督学习出来的语法结构往往不符合人类的语言学直觉。
3. 2.4.1 Supervised Vs. Unsupervised
| 特性 | 有监督训练 (Supervised) | 无监督训练 (Unsupervised) |
|---|---|---|
| 数据需求 | 句子 + 句法树 (Treebank) | 仅句子 (Raw Text) |
| 核心方法 | MLE (数数) | EM (Inside-Outside) |
| 计算复杂度 | 低,遍历一遍即可 | 高,需要反复迭代 |
| 准确率 | 高 (直接学习标准答案) | 较低 (容易陷入局部最优) |
| 应用场景 | 主流工业界应用 (如 Stanford Parser) | 探索性研究,或辅助有监督训练 |
2.3 依存句法分析
依存句法分析(Dependency Parsing)
依存句法分析是自然语言处理中的核心任务之一,其目标是依据依存语法理论,分析输入的句子并自动构建出其对应的依存句法结构树。依存句法理论的基本假设是:句法结构本质上由单词与单词之间的二元关系组成。这种关系是非对称的,具有方向性,从中心语(Head)指向依存成分(Dependent)。
在形式化表示中,我们通常将依存句法结构视为一个依存图(Dependency Graph) $G = (V, A)$。其中,$V$ 是顶点集合,包含输入句子中的所有单词 $w_1 \dots w_n$ 以及一个虚拟的根节点 $ROOT (w_0)$;$A$ 是边集合(Arcs),代表单词间的依存关系,通常带有表示语法关系(如主语、宾语)的标签。一个合法的依存句法分析结果必须是一个从 $ROOT$ 出发的有向树,且必须覆盖句子中的每一个单词(即每个词有且仅有一个中心语,ROOT 除外)。
2.4 基于图的依存句法分析框架
在实际算法层面,课件中主要介绍的是**基于图(Graph-based)的分析方法。这种方法的核心思想是将句法分析问题转化为图论中的最大生成树(Maximum Spanning Tree, MST)**问题。
其基本逻辑是构造一个评分函数,对依存图中的每一条可能的边进行打分。对于一个给定的句子 $S$,我们需要在所有可能的句法树集合中,找到一棵树 $G$,使得这棵树上所有边的得分总和最大。形式化表示为:
$\hat{G} = \arg\max_{G \in \mathcal{G}S} \sum{(w_i, w_j) \in A} \text{score}(w_i, w_j)$
其中,$\text{score}(w_i, w_j)$ 代表建立从词 $w_i$ 到词 $w_j$ 的依存关系的可能性。
根据语言是否允许依存弧线交叉(即是否满足投射性),算法分为两类:
2.4.1 非投射性依存句法分析
当语言允许依存弧线交叉时(这在语序自由的语言中很常见),我们需要寻找有向图的最小/最大生成树。课件中重点介绍了朱-刘/埃德蒙兹算法(Chu-Liu/Edmonds Algorithm)。
该算法的执行步骤如下:
第一步,贪心选择:对于图中的每一个节点(除 ROOT 外),选择一条入边权重最大的边,构成子图 $G’$。
第二步,环路检测:检查 $G’$ 中是否存在环。如果不存在环,则 $G’$ 即为最大生成树,算法结束。
第三步,缩环(Contraction):如果存在环,将该环缩成一个“超级节点”。
第四步,权重调整与递归:调整指向该超级节点的外部边的权重,并在新图上递归调用上述过程寻找最大生成树。
第五步,展开(Expansion):得到缩环图的树后,将超级节点展开回原来的环,并移除环内与外部入边冲突的那条边,恢复原始结构。
2.4.2 投射性依存句法分析
如果假设语言满足投射性(Projectivity),即依存弧线在单词上方绘制时互不交叉,那么依存句法树等价于嵌套依存树(Nested Dependency Trees)。
在这种约束下,我们可以利用其与上下文无关文法(CFG)的相似性,采用类似 CKY 算法 的动态规划(Dynamic Programming) 方法。
我们定义动态规划表 $C[s][t][i]$,表示以单词 $w_i$ 为根节点,覆盖从单词 $w_s$ 到 $w_t$ 的连续子片段的最高得分。算法通过从小片段合并成大片段的方式(自底向上),计算出覆盖整个句子且以 ROOT 为根的最高分。
2.5 基于神经网络的方法
传统的图分析方法依赖人工特征工程来计算边的得分。现代方法则使用神经网络来自动提取特征并计算评分,主要包括:
2.5.1 基于双仿射变换
该模型引入了双向长短时记忆网络(BiLSTM)来对句子的上下文信息进行建模。它将单词的词嵌入和词性嵌入合并作为输入。在评分阶段,使用**双仿射(Biaffine)**注意力机制来计算两个词之间存在依存关系的得分以及具体关系标签的得分。这种方法极大地提高了评分的准确性。
2.5.2 基于图神经网络(GNN)
为了利用更多的结构化信息,可以引入图神经网络(Graph Neural Networks)。这种方法试图在节点表示中融入局部甚至全局的依存结构信息,从而更精准地进行预测。
2.6 Evaluation
,评估(Evaluation) 是一个至关重要的环节。我们需要一种标准化的方法来衡量一个 Parser 生成的树到底有多好。
2.6.1 成分句法分析的评估
这部分内容集中在课件 Page 121-123。
1. 核心理念:括号化
我们不能简单地看整棵树是否完全一样(Exact Match),因为树太复杂了,只要错一个地方,整棵树就“错”了,这样太严苛。
因此,我们将一棵树拆解为若干个成分(Constituents/Brackets)。
一个成分由三个要素唯一确定:Start(起始位置), End(结束位置), Label(非终结符标签)。
- Gold Standard (金标准/标准答案): 人工标注的正确树中的成分集合。
- Candidate (候选结果): Parser 跑出来的树中的成分集合。
2. 具体指标 (Metrics)
我们通过比较 Candidate 和 Gold Standard 集合的重叠程度来计算以下指标:
Labeled Precision (LP, 标记精确率):
Parser 找出的成分中,有多少是正确的?
$$LP = \frac{\text{Parser 预测正确的成分数}}{\text{Parser 预测出的总成分数}}$$Labeled Recall (LR, 标记召回率):
标准答案里的成分,Parser 找出了多少个?
$$LR = \frac{\text{Parser 预测正确的成分数}}{\text{标准答案的总成分数}}$$F1 Score (LP 和 LR 的调和平均数):
综合衡量指标。
$$F1 = \frac{2 \times LP \times LR}{LP + LR}$$Tagging Accuracy (词性标注准确率):
叶子节点上的词性标记(POS Tags)对不对?这是一个底层的辅助指标。
3. 实例演算
让我们用 PPT 中的例子来实操一下:
- Gold Standard (8 个成分):
S-(0:11),NP-(0:2),VP-(2:9),VP-(3:9),NP-(4:6),PP-(6-9),NP-(7,9),NP-(9:10) - Candidate (7 个成分):
S-(0:11),NP-(0:2),VP-(2:10),VP-(3:10),NP-(4:6),PP-(6-10),NP-(7,10)
计算过程:
找交集(Correct): 也就是两者一模一样的成分。
S-(0:11): ✅NP-(0:2): ✅NP-(4:6): ✅- 其他都不匹配(注意:即使范围对了但 Label 错了,或者 Label 对了范围错了,都不算)。
- 正确数 = 3
计算 Precision:
- $LP = 3 (\text{Correct}) / 7 (\text{Candidate Total}) = 42.9%$
计算 Recall:
- $LR = 3 (\text{Correct}) / 8 (\text{Gold Total}) = 37.5%$
计算 F1:
- $F1 \approx 40.0%$
**4. 现状 **
- 普通的 Vanilla PCFG 在 Penn Treebank 上的 F1 分数大约是 73%。
- 这个分数不够好,主要原因是它缺乏**词汇化(Lexicalization)**信息(即不知道具体单词的搭配习惯),这也是后续课程引入 Lexicalized PCFG 的原因。
2.6.2 依存句法分析的评估
核心指标:
UAS (Unlabeled Attachment Score, 无标记依存准确率):
- 只看箭头指没指对(即中心语 Head 找没找对)。
- 公式:$\frac{\text{找对中心语的词数}}{\text{总词数}}$
LAS (Labeled Attachment Score, 有标记依存准确率):
- 要求更高:不仅**箭头(Head)要指对,箭头上写的关系标签(Relation,如 nsubj, dobj)**也要对。
- 这是最常用的核心指标。
CM (Complete Match, 完全匹配率):
- 整个句子的依存结构完全正确的比例(只要错一根线就算错)。
- 成分句法(CFG/PCFG) 评估的核心是 Range + Label(范围+标签),看的是**块(Constituents)**的重合度,指标是 LP/LR/F1。
- 依存句法 评估的核心是 Head + Relation(指向+关系),看的是**边(Arcs)**的准确度,指标是 UAS/LAS。