正则化表达
- 字母
| Pattern | Matches |
|---|---|
| [wW]oodchuck | Woodchuck, woodchunck |
| 1 2 3 4 5 6 7 8 9 | Any digit |
- 范围 [A-Z]
| Pattern | Matches | |
|---|---|---|
| [A-Z] | 大写字母 | Drenched Blossoms |
| [a-z] | 小写字母 | my beans were impatient |
| [0-9] | 单个数字 | Chapter 1: Down the Rabbit |
- 否定 [^Ss]
^仅作用[]中的第一个字符
| Pattern | Matches | |
|---|---|---|
| [^A-Z] | 非大写字母 | Oyfn pripetchik |
| [^Ss] | 既不是S也不是s | I hava no exquisite reason” |
| [^e^] | 既不是e也不是^ | Look here |
| a^b | 表示 a^b | Look up a^b now |
- 分离 |
| Pattern | Matches |
|---|---|
| groundhog|woodchuck | |
| yours|mine | yours mine |
| a|b|c | = [abc] |
| [gG]roundhog|[Ww]oodchuck |
- ? * + .
| Pattern | Matches | |
|---|---|---|
| colou?r | 匹配前一个字符0次或者1次 | coolor colour |
| oo*h! | 0或更多前一个字符 | oh! ooh! oooh! |
| o+h! | 1或更多前一个字符 | oh! ooh! oooh! |
| baa+ | baa baaa baaaa | |
| beg.n | 任意字符 | begin begun beg3n |
- Anchors
匹配位置
| Pattern | Matches | |
|---|---|---|
| ^[A-Z] | 大写字母开头 | Palo Alto |
| ^[^A-Za-z] | 非字母开头 | 1 “Hello” |
| \.$ | 必须以.结尾 | The end. |
| .$ | 匹配任意一个字符 | The end? The end! |
- More
| Pattern | Matches |
|---|---|
| a(bc){2,4} | abbcbc or abcbcbc or abcbcbcbc |
| {2,} | 2 or more |
| {,6} | up to 6 |
| {3} | exactly 3 |
| [] | 表示该集合中的任意一个字符 |
| inside [] | 在[]内部符号不再有特殊含义 |
- 内置的常见字符

Grammars
Languages: 抽象的符号集合
Grammars:一组规则或者说是一个枚举器,用来生成语言中合法的句子
考虑一个简单语法(上下文无关文法):
S → aSb | ε
这个语法能生成: ε(空串) ab aabb aaabbb ...→ 它定义了一个语言:所有形如 a^n b^n 的字符串(n ≥ 0)
这个语法就是一个“枚举器”,它能一步步生成所有合法句子。
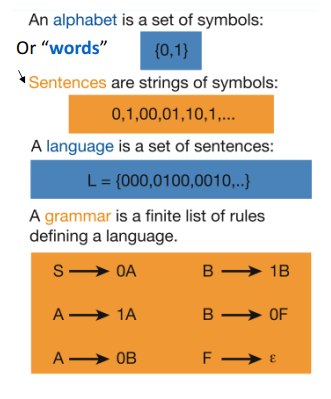
文法的形式化定义:
G = (V_T,V_N,P,S)
- V_T:终结符, 文法所定义语言的基本符号。{apple, boy,eat,little}
- V_N:非终结符,用来表示语法成分的符合。{<句子>,<名词短语>,<动词短语>,<名词>}
- P:产生式,描述了将终结符和非终结符组合成串的方法。<句子> -> <名词短语><动词短语>
- S:开始符合,表示文法中最大的语法成分。S=<句子>
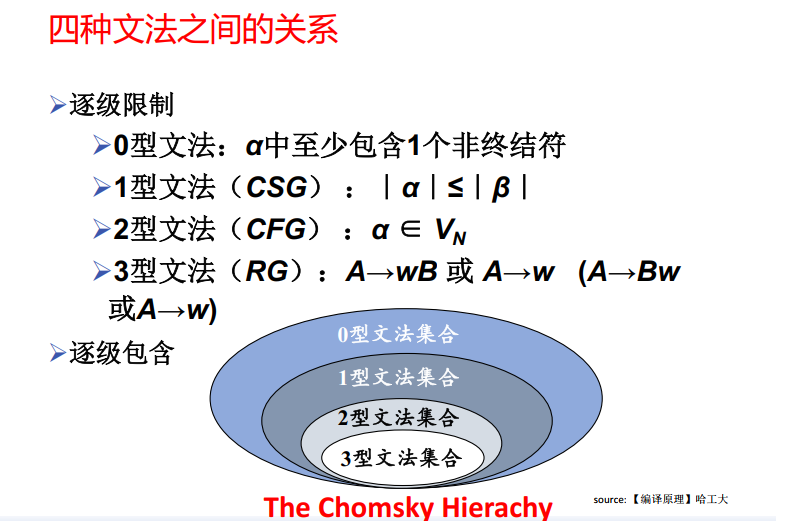
- 0型文法, 又称无限制文法,$\alpha \to \beta$,唯一的限制是规则左侧至少包含一个非终结符
- 1型文法,又称上下文有关文法。$\alpha_1 A \alpha_2 \to \alpha_1 \beta \alpha_2$ 限制右侧长度不小于左侧长度
- 2型文法,又称上下文无关文法。$A \to \beta$、
- 3型文法,又称正则文法。正则文法要求产生式规则必须是线性的,这意味着在规则的右侧,最多只能出现一个非终结符,并且这个非终结符的位置必须是固定的(要么在最左边,要么在最右边)
- 右线性文法:$A \to wB $ or $A\to w$
- 左线性文法:$A \to Bw$ or $A \to w$
正则表达匹配
The Chomsky Hierachy:乔姆斯基层次结构
Finite Automata
有限自动机等价于 3型文法,有 DFA:确定的有穷自动机,NFA 非确定的有穷自动机两种。
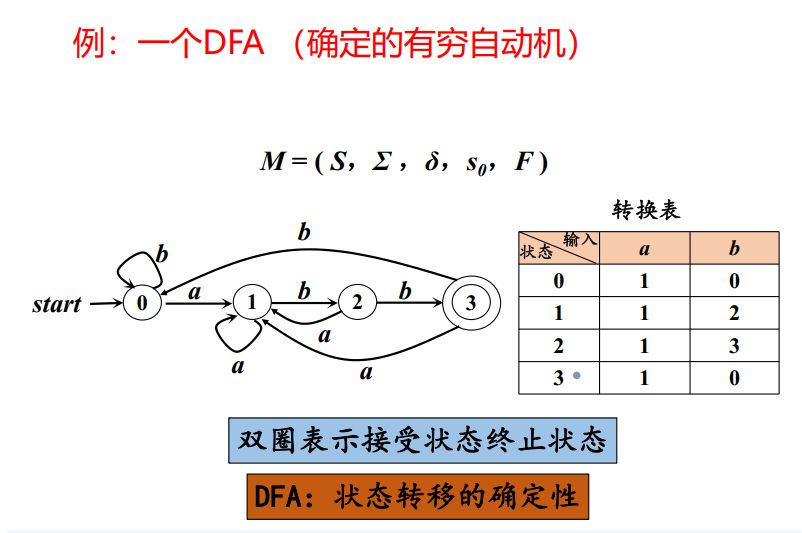
$$M = (Q, \Sigma, \delta, q_0, F)$$
这五个组成部分分别代表了自动机的各个方面:
- $Q$: 有穷状态集 (Finite set of States)
- 定义: 自动机在运行过程中可能处于的所有状态的集合。
- 特性: $Q$ 必须是有限的。这是 有限自动机 名称的由来,也限制了它能“记住”的信息量是有限的。
- $\Sigma$: 输入字母表 (Input Alphabet)
- 定义: 自动机能够识别和处理的所有有效输入符号的集合。
- 特性: $\Sigma$ 也是一个有限集合。
- 注意: 幻灯片明确指出 “假设 $\epsilon$ 不是 $\Sigma$ 中的元素“。 $\epsilon$ 代表空串,因为它不消耗输入符号,在确定有限自动机 (DFA) 的定义中,它不作为常规输入符号。
- $\delta$: 转换函数 (Transition Function)
- 定义: 它是一个映射函数,定义了自动机在读取一个输入符号时,从一个状态转移到下一个状态的规则。
- 形式: $\delta: Q \times \Sigma \to Q$
- 它将当前状态(来自 $Q$)和输入符号(来自 $\Sigma$)的组合,映射到下一个状态(来自 $Q$)。
- DFA 的确定性体现在: 对于任意的状态 $s \in Q$ 和任意的输入符号 $a \in \Sigma$,$\delta(s, a)$ 唯一地确定了下一个状态。
- $q_0$: 开始状态 (Start State)
- 定义: 自动机开始执行计算时的初始状态。
- 特性: $q_0$ 必须是状态集合 $Q$ 中的一个元素。
- $F$: 接受状态集 (Set of Final/Accepting States)
- 定义: 当输入字符串被完全读取后,如果自动机停在 $F$ 中的某个状态,则表示该字符串被接受。
- 特性: $F$ 是状态集合 $Q$ 的一个子集 ($F \subseteq Q$)。
DFA的确定指的是下一个状态确定,有三个部分:
- 单向、无限长的纸带 (One-way, infinite tape, broken into cells)
- 单向、只读的读头 (One-way, read-only tape head)
- 有限控制 (Finite Control)
NFA: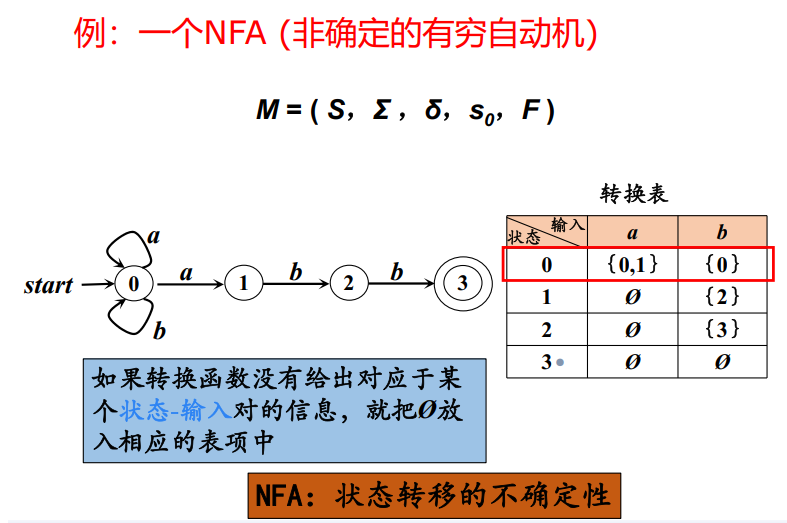
NFA到DFA的转换
DFA中的每个状态都是一个由NFA中的状态构成的集合,即NFA转态集合的一个子集,我们可以通过子集构造法:
Push-Down Automata(PDAs)
下推自动机与2型文法等价。通过添加无界的内容,但以首先得方式访问(即添加一个栈)。
很好,让我们来学习下推自动机 (PDA) 的形式化定义。
由于 PDA 比 DFA 多了一个栈结构,它的形式化定义也比 DFA 的五元组更加复杂,需要七个元素。
下推自动机 (PDA) 的形式化定义
一个下推自动机 $M$ 通常被定义为一个 七元组:
$$M = (Q, \Sigma, \Gamma, \delta, q_0, Z_0, F)$$
详细说明
- $Q$: 有穷状态集 (A finite set of states)
- 定义: 自动机内部的有限状态集合。
- 示例: 在句法分析中,状态可以代表解析过程中到达的某个中间步骤。
- $\Sigma$: 输入字母表 (A finite alphabet of input symbols)
- 定义: 所有可接受的输入符号的集合。
- $\Gamma$: 栈字母表 (A finite alphabet of stack symbols)
- 定义: 唯一属于 PDA 的新元素。它是所有可以存储在栈中的符号的集合。
- 特性: 栈字母表 $\Gamma$ 可以包含输入字母表 $\Sigma$ 中的符号,也可以包含额外的非终结符等特殊符号。
- $q_0$: 初始状态 (An initial (start) state)
- 定义: 自动机开始执行时的状态,属于 $Q$。
- $Z_0$: 初始栈符号 (An initial (start) stack symbol)
- 定义: 栈中最初放置的符号,代表栈的底部。
- 特性: $Z_0$ 必须属于栈字母表 $\Gamma$。它的存在是为了方便判定栈是否为空。
- $F$: 终止状态集 (A set of final states)
- 定义: 接受状态的集合,属于 $Q$ 的子集。
- $\delta$: 转换函数 (A transition function)
定义: PDA 的核心,定义了从一个状态到另一个状态的转移规则,并规定了栈的操作。
形式: $\delta: Q \times (\Sigma \cup {\epsilon}) \times \Gamma \to $ 有限集 $(Q \times \Gamma^*)$
规则左侧(输入): 当前状态 $\times$ 输入符号(可以是 $\epsilon$) $\times$ 栈顶符号
- $\Sigma \cup {\epsilon}$: 允许 $\epsilon$-转移(不读取输入符号,只进行栈操作和状态转移)。
规则右侧(输出): 下一个状态 $\times$ 压入栈的新符号串($\Gamma^*$,可以是空串 $\epsilon$ 来实现弹出)。
Demo: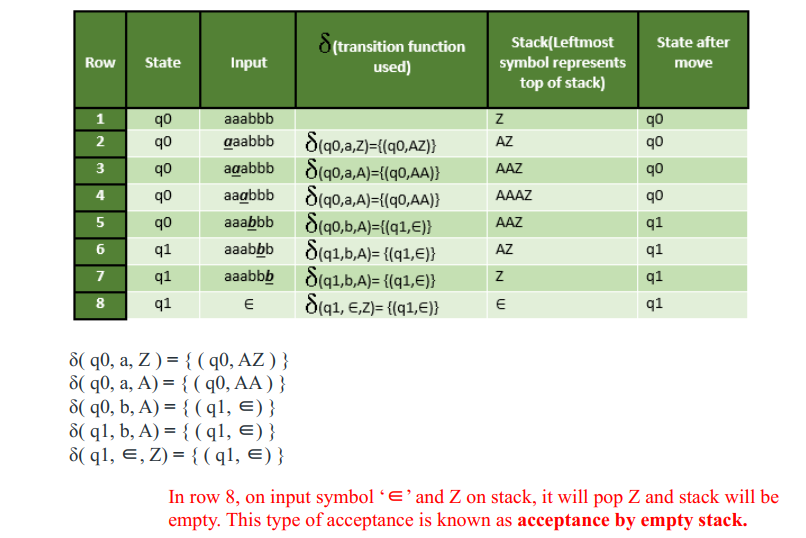
Turing Machines
图灵机等价于0型文法,核心结构:
- 无限长的纸带 (Tape)
- 读写头 (Head)
- 有限控制单元 (Control Unit)
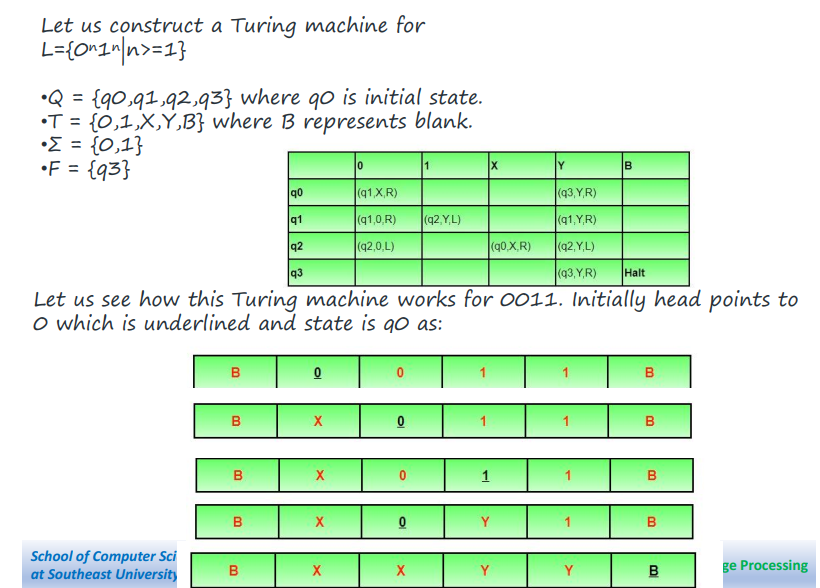
参考资料
哈工大编译原理