1.Background
边缘特征:图像强度发生突变的地方
我们使用偏导数来设计一个滤波器:例如[-1, 1]用来计算水平方向的亮度变化,最后展示的是竖直方向的条纹
Finite difference filters(有限差分滤波器),有如下三种
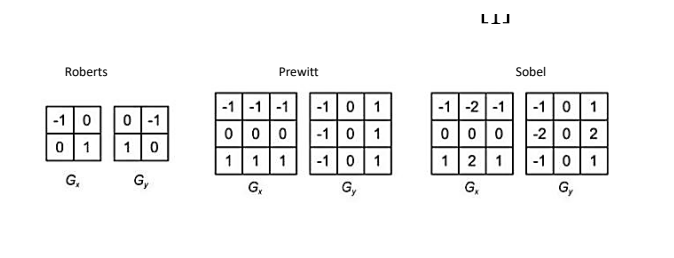
最常用的是Sobel滤波器,它是由 $ [1,2,1]^T $$ [-1,0,1] $得到的,本质上是左边乘了一个高斯平滑
噪声影响:一阶导数也会呈现密集的上下波动
解决方案:先平滑(乘上一个高斯函数进行平滑操作),再进行求导 $ \frac{d(fg)}{dx} = f \frac{dg}{dx} $,说明我们也可以先对高斯函数求导再进行平滑,结果是一样的,下图为高斯滤波器的导数。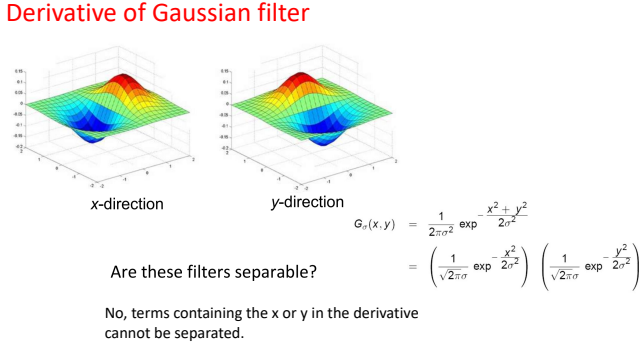
注意:导数中的x, y不可以分割
高斯平滑可以去除噪声,但是当scale越大的时候,图像也就越模糊
Sobel Filter Problem
- 定位不准确
- 阈值化参数倾向于特定的方向,会错过更多的斜边缘
2.Canny Detector
Canny edge detector

- 解决如何将粗大的线条变成细线条
解决方案:非极大值抑制:检查像素是否沿着梯度方向的最大值,选择边缘宽度上的最大值
- 一些边缘由于低于阈值而不能显示
解决方案:使用高阈值开始绘制边缘,再使用低阈值将边缘连接
高斯kernel中 $ \sigma $的影响
- $ \sigma $越大,图像越模糊,只剩下大致轮廓
- $ \sigma $越小,图片更加清晰,保留细节更多
3.双边滤波
Bilateral Filter:双边滤波
主要处理高斯滤波处理噪声的时候将边缘也模糊化的问题
- Spatial:距离越近,权重越大
- Brightness:亮度越近,权重越大
公式:
$ BF[I]p = \frac{1}{W_p} \sum{q \in S} \underbrace{G_{\sigma_s}(||p - q||)}{\text{Space Weight}} \underbrace{G{\sigma_r}(|I_p - I_q|)}_{\text{Range Weight}} I_q $
我们把这个公式拆解开来看,它由两部分高斯函数相乘组成:
- Space Weight (空间权重 $ G_{\sigma_s} $):
- 公式部分:$ G_{\sigma_s}(||p - q||) $
- 含义:像素位置 $ p $ 和 $ q $ 的距离。
- 作用:离得越近,关系越好(这就是普通的高斯模糊)。
- Range Weight (值域/亮度权重 $ G_{\sigma_r} $):
- 公式部分:$ G_{\sigma_r}(|I_p - I_q|) $
- 含义:像素亮度 $ I_p $ 和 $ I_q $ 的差异。
- 作用:长得越像(颜色越近),关系越好。如果颜色差很多(比如遇到了边缘),这一项的值会迅速变成 0。
4.深度学习方法
Deep learning-based solutions for low-level vision tasks
Low-quality images procession
Predict the blur kernel
- End-to-End prediction –multi-scale fusion
- End-to-End prediction –CNN+Transformer
- A generation view – multi-scale generator
- Task-specific constraints
Edge detection
- Patch-wise classification
- Multi-sacle connection strategies(End-to-End prediction –Multi-scale learning)
- End-to-End prediction – level-specific supervision –enhance the details
- CNN+Edge filters
- CNN+Transformer