主要问题:噪声、离散值、遮挡
| 场景/问题 (Scenario) | 具体情况 (Context) | 解决方案/算法 (Method) |
|---|---|---|
| 基础拟合 | 如果我们已经明确知道哪些点属于这条线,想找到最优的直线参数。 | 最小二乘法 (Least squares) |
| 处理干扰 | 如果数据中混杂了离群点 (Outliers)(比如噪点、错误匹配)。 | 鲁棒拟合 (Robust fitting) RANSAC |
| 多目标检测 | 如果图像中不止一条线,而是存在很多条线。 | 投票法 (Voting methods): 1. RANSAC 2. 霍夫变换 (Hough transform) |
| 模型不确定 | 如果我们甚至不确定目标是不是直线(可能是圆、曲线等)。 | 模型选择 (Model selection) |
Least squares
Total least squares
- 普通最小二乘法:无法处理垂直问题,不具有旋转不变性
- Total least squares(正交回归):使用 $ ax+by=d $一般式子,我们计算正交距离$ E = \sum (ax_i + by_i -d)^2 $,正交距离具有旋转不变性
Robust Estimators
当出现离群点的时候,这一两个点回极大的影响线形模型的鲁棒性,我们引入了鲁棒估计(Robust Estimators)。
核心思想:
我们要修改“惩罚规则”。我们不再使用简单的“平方误差”,而是设计一个新的函数 $ \rho $,让它对巨大的误差**“视而不见”**。
公式解读:
$ \rho(u; \sigma) = \frac{u^2}{\sigma^2 + u^2} $
- $ u $:残差(点到线的距离)。
- $ \sigma $:一个尺度参数(控制我们对误差的宽容度)。
看下面那张曲线图(非常重要):
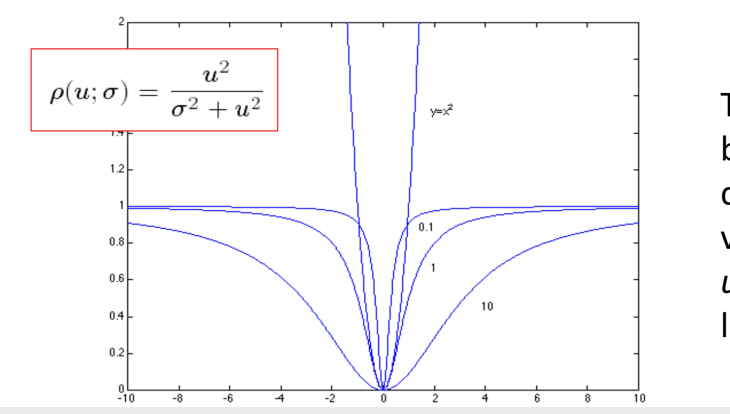
这张图画的就是上面这个函数 $ \rho $ 的形状。
- 横轴是误差 $ u $(点离线有多远)。
- 纵轴是惩罚值(Cost)。
这个函数有两个性格:
- 当误差 $ u $ 很小的时候(中间凹下去的部分):
- 它长得像一个抛物线($ y=x^2 $)。
- 含义: 对于靠近直线的“好点”,我们依然像最小二乘法一样,希望它们越准越好。
- 当误差 $ u $ 很大的时候(两边变平的部分):
- 曲线**饱和(Saturates)**了,变平了,趋近于 1。
- 含义: 这就是魔法所在!如果一个点离线非常远(比如之前的那个离群点),原本最小二乘法会给它判一个巨大的罚分(比如25),但现在这个函数说:“算了吧,不管你离多远,我就给你记个上限值 1”。
- 既然最大的惩罚也才只有 1,算法就不会为了迁就这个坏点而牺牲整条直线了。
- 鲁棒估计拟合是一个非线性优化问题,必须使用迭代方法求解。
- 可以用最小二乘法进行初始估计
- 根据中位数残差适当地选择比例因子
RANSAC
Definition
计算机视觉中最著名、最常用的算法之一:RANSAC (Random Sample Consensus,随机采样一致性)。
如果说上一节讲的“鲁棒估计器(M-estimator)”是对最小二乘法的改良,那么 RANSAC 就是一种彻底的颠覆。
以下是核心解读:
1. 为什么要发明 RANSAC?
- 第一点: “Robust fitting can deal with a few outliers – what if we have very many?”
- 背景: 之前的鲁棒方法(比如 M-estimators)虽然能处理一些离群点,但它们基于梯度下降或迭代优化,如果数据里的垃圾(离群点)实在太多(比如超过 50% 都是噪声),这些方法很容易陷入局部最优解,导致失败。
- RANSAC 的使命: 它是专门为了应对极其恶劣的数据环境而生的。哪怕你的数据里有一半以上都是垃圾,RANSAC 依然能把正确的模型找出来。
2. RANSAC 的核心逻辑:与其“妥协”,不如“赌博”
普通的最小二乘法试图让所有点都满意(平均误差最小)。
RANSAC 的逻辑完全不同:它假设大部分数据可能都是垃圾,我只信任我随机选中的那几个点。
3. 算法流程 (Outline) - 通俗翻译
PPT 列出了 RANSAC 的四个标准步骤,我们可以把它想象成一次**“海选投票”**的过程:
- 第一步:随机抽样 (Choose a small subset)
- 从所有数据点中,随机抽取最少数量的点。
- 例子: 如果你要检测直线,两点确定一条直线,所以就随机抽 2 个点。
- 关键: 只抽最少的,绝不多抽,为了降低抽到坏点的概率。
- 第二步:建立假设 (Fit a model)
- 假设刚才抽到的这 2 个点是完美的“好点”,用它们算出一个模型(比如画出一条直线)。
- 第三步:验证一致性 (Find all remaining points…)
- 这是最关键的一步。拿着刚才那条直线,去测试数据集中剩下所有的点。
- 问每一个点:“你离这条线近吗?”
- 如果距离小于某个阈值,这个点就投一票(算作内点/Inlier)。
- 如果距离很远,这个点就被视为离群点/Outlier,直接忽略。
- 统计票数: 记下这条直线一共获得了多少个内点的支持。
- 第四步:循环择优 (Do this many times)
- 因为第一步是随机抽的,运气不好可能抽到了落叶(离群点),导致画出来的线很烂,没几个点支持它。
- 所以,我们要把上述过程重复 N 次(比如重复 100 次)。
- 最终结果: 在这 100 次尝试中,哪条直线获得的票数(内点数)最多,我们就认为那条直线是最终的最佳模型。
Parameters
如何选择超参数?
- 初始样本数量 $ s $:通常模型选取的样本数量越少越好,因为混入的离群点的概率就越小
- 距离阈值 $ t $:判断一个点是不是“内点” 还是 “离群点” 的标准,通常根据预期的噪声水平来确定
- 定义: 判定一个点是否支持当前模型的距离门槛。
- 怎么定? 基于统计学原理(卡方分布)。
- 公式解读: $ t^2 = 3.84\sigma^2 $
- 假设测量误差服从高斯分布(正态分布),标准差是 $ \sigma $。
- 统计学告诉我们,如果设定阈值为 $ 1.96\sigma $(大约2倍标准差),那么理论上 95% 的真正内点都会落在这个范围内。
- $ 1.96^2 \approx 3.84 $。
- 通俗做法: 如果你估计你的特征点定位误差大概是 1 个像素 ($ \sigma=1 $),那你的阈值 $ t $ 就设为 $ \sqrt{3.84} \approx 2 $ 个像素。超过 2 像素的误差就不认了。
- 采样次数 $ N $:我们不希望无限循环,希望有99%的把握至少有一次抽样是完全干净的
公式推导逻辑:
- 设 $ e $ 为离群点比例(比如 20% 的数据是垃圾, $ e=0.2 $)。
- 那么,随机抽 1 个点,它是好点的概率是 $ 1-e $。
- 我们需要连续抽 $ s $ 个点都是好点,概率是 $ (1-e)^s $。
- 反过来,抽样失败(抽的 $ s $ 个点里至少混进了一个坏点)的概率是 $ 1 - (1-e)^s $。
- 如果我们重复抽了 $ N $ 次,每一次都失败了(运气极差),这个概率是 $ (1 - (1-e)^s)^N $。
- 我们希望这个“彻底失败”的概率非常非常小,小到只有 $ 1-p $(比如 0.01)。
- 于是得到公式:
$ (1 - (1-e)^s)^N = 1 - p $
- 求解 $ N $: 通过取对数,就得到了下面那个计算 $ N $ 的公式:
$ N = \frac{\log(1-p)}{\log(1-(1-e)^s)} $
进阶策略:自适应
- 痛点: 现实中,我们往往根本不知道 $ e $(离群点比例)是多少。随便猜一个 50%?万一实际只有 10% 垃圾,那你岂不是白白多算了几百次?
- 解决方案: 边跑边改!
- 初始状态: 假设情况最糟糕,设 $ e=100% $(或者一个很大的值),此时 $ N $ 是无穷大。
- 开始循环: 每次抽样拟合出一个模型,数一数有多少个内点。
- 动态更新:
- 假设第 5 次循环时,你运气爆棚,找到了一条直线,发现竟然有 80% 的点都支持它。
- 这说明真实的离群点比例 $ e $ 最多 只有 $ 20% $ ($ 1 - 0.8 $)。
- 赶紧把这个新的 $ e=0.2 $ 代入公式,重新计算 $ N $。
- 你会发现 $ N $ 瞬间变小了(比如从 1000 变成了 20)。
- 提前终止: 如果你当前的循环次数
sample_count已经超过了新计算出来的 $ N $,那就直接收工!
- 投票数量 $ d $:这是一个终止条件。
Pros vs. Cons
| 分类 | 中文 |
|---|---|
| 优点 (Pros) | 简单且通用: 算法的核心逻辑(采样-验证-循环)非常简单,且不局限于直线检测,可以套用到任何数学模型的拟合中。 |
| 适用范围广: 无论是拼图(单应性矩阵)、物体识别(仿射变换)还是形状检测(圆、椭圆),它都能处理。 | |
| 实战效果好: 在真实世界充满噪声和干扰的数据中,它通常都能稳定地找到正确模型,鲁棒性很强。 | |
| 缺点 (Cons) | 参数调优麻烦: 你需要手动设置**迭代次数 **$ N $、**距离阈值 **$ t $、**采样点数 **$ s $ 等。这些参数没有标准答案,需要根据具体场景去试。 |
| 对低内点率(垃圾数据太多)敏感: 如果数据中“好点”的比例极低(比如只有 10% 是好点),根据之前的公式,需要的迭代次数 $ N $ 会呈指数级爆炸,导致计算太慢或者直接算不出结果。 | |
| 初始化未必总是好的: 因为我们是用“最少点数”(比如2点)来定模型。如果这2个点虽然是内点,但本身带有噪声(比如靠得太近),算出来的初始模型可能偏差很大。 |
Hough transform
Definition
我们要从 RANSAC(随机猜测法)转向 霍夫变换(Hough Transform,基于投票的方法)。
这是为了解决 RANSAC 在特定场景下的局限性,特别是面对“鹦鹉笼子”这种复杂图片时。

场景分析:
左边的图是一只关在笼子里的鹦鹉。我们的任务是检测出笼子的铁丝网(直线)。
RANSAC 在这里会遇到的两个致命问题:
- 多条直线 (Multiple lines):
- RANSAC 的逻辑是“一次找一条最强的线”。
- 笼子有几十条横线和竖线。如果你用 RANSAC,它可能找到了其中一根竖线,然后把这根线剔除,再跑一遍找下一根……这样效率极低,而且很难判断什么时候停下来。
- 离群点太多 (Too many outliers):
- 这是最关键的。对于笼子里的某一根特定铁丝来说,其他所有的铁丝以及鹦鹉本身,全都是“干扰项(Outliers)”。
- 这意味着,针对某一条线,可能有 95% 的数据都是噪声。
- 还记得上一张 PPT 的公式吗?当 $ e $(离群率)很高时,$ N $(需要的循环次数)会呈指数级爆炸。RANSAC 在这种情况下几乎跑不动,或者很难抽中那两个完美的点。
右边的图是什么?
那张黑底白亮斑的图,就是霍夫变换的结果(霍夫空间/参数空间)。
- 每一个亮点,就代表检测到了一条直线。
- 你可以看到有很多亮点,这意味着算法一次性就把所有笼子的线条都找出来了。
为了解决上面的问题,我们换一种思路:不再去“猜”模型(RANSAC),而是让数据自己“投票”选出模型。
核心哲学:
- 让每个特征点投票 (Let each feature vote):
- 图像上的每一个边缘点(比如笼子上的一点),都去“思考”:有哪些直线可能穿过我?
- 它给所有可能的直线都投一票。
- 噪声无法形成合力 (Noise features will not vote consistently):
- 关键点! 鹦鹉身上的羽毛也是边缘点,也会投票。但是,羽毛是杂乱无章的。
- 羽毛 A 投给直线 X,羽毛 B 投给直线 Y。它们的票是分散的,无法在某一个特定的候选直线由于上形成高票。
- 相反,笼子上的点虽然断断续续,但它们都整齐地排列在一条直线上,它们都会投给同一个候选人。
- 不怕缺失数据 (Missing data doesn’t matter):
- 结合鹦鹉图: 鹦鹉的身体挡住了笼子中间的部分(Occlusion)。
- 在投票机制下,这没关系。只要笼子上半部分的点投了票,下半部分的点也投了票,这两个部分的票加在一起,依然能让这条直线胜出。算法会自动“脑补”出被鹦鹉挡住的那部分线条。
总结
- RANSAC 适合:只有 1 个主要模型,且只有少部分噪声的情况。
- 霍夫变换 适合:有多个模型(如很多条线),且噪声很大/遮挡严重的情况。它利用“少数服从多数”的投票原理,让真正的直线在噪声中脱颖而出。
Parameters space representation
参数空间表示
- 直线映射到霍夫空间一个点
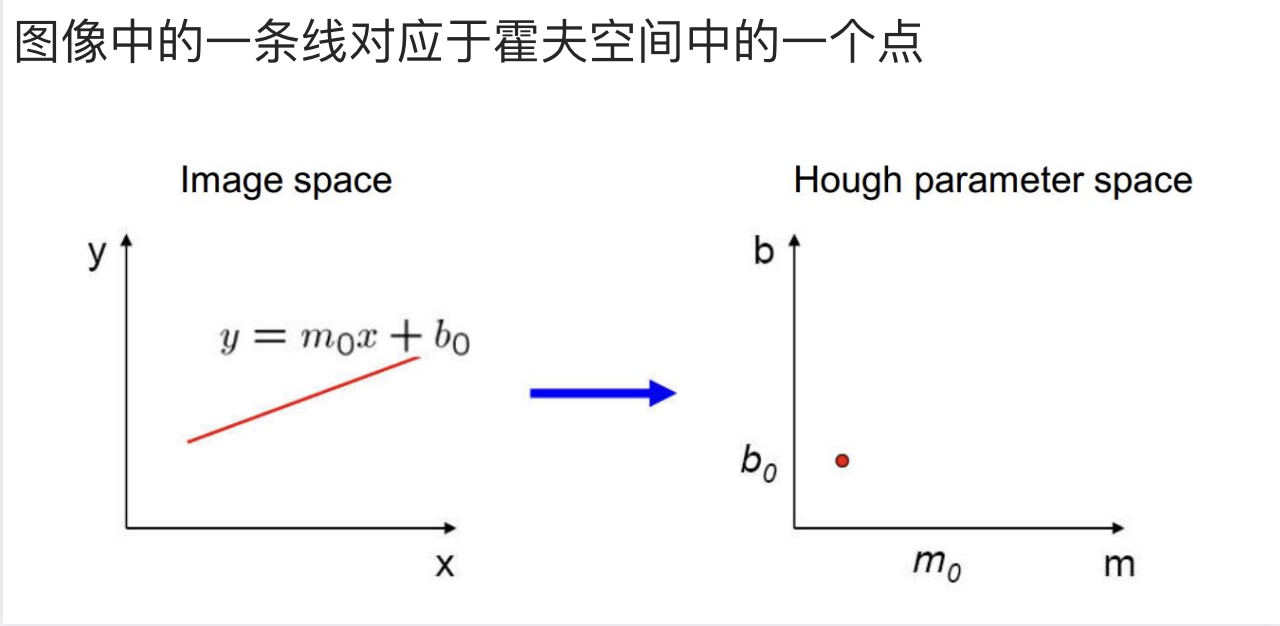
- 点映射到霍夫空间的一条直线
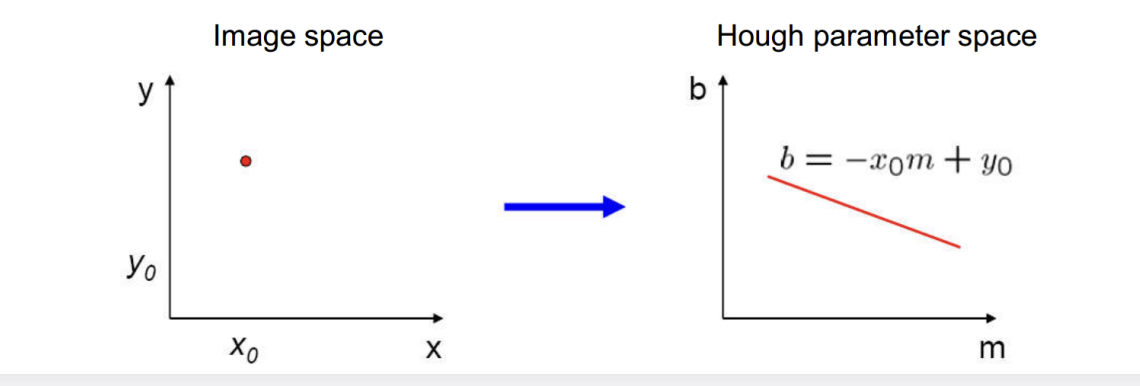
- 包含两个点的直线
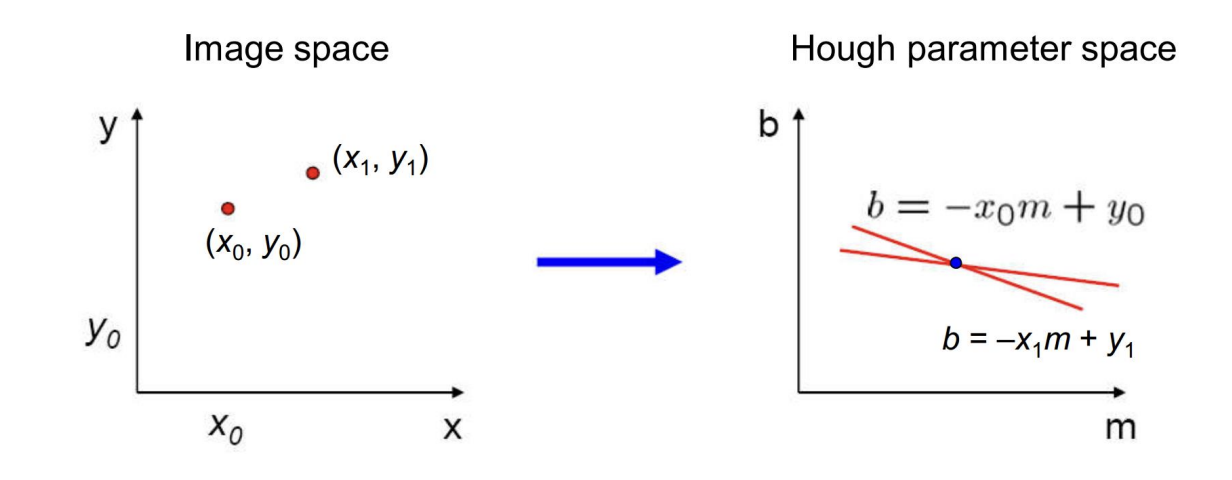
Polar representation
极坐标表示:
传统的斜截式方程存在着一些问题:1.垂直线的斜率是无穷大;2.只有线很陡,斜率的参数就会非常大,内存可能会爆炸。
我们使用极坐标$ x \cos \theta + y \sin \theta = \rho $ ,将无界空间变为来有界空间
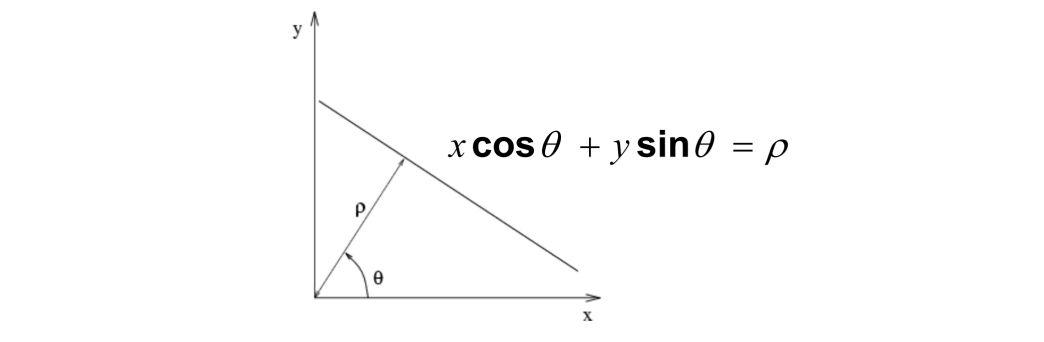
在极坐标的空间里,每个点被映射为了一个正弦曲线
Basic algorithm
算法流程:
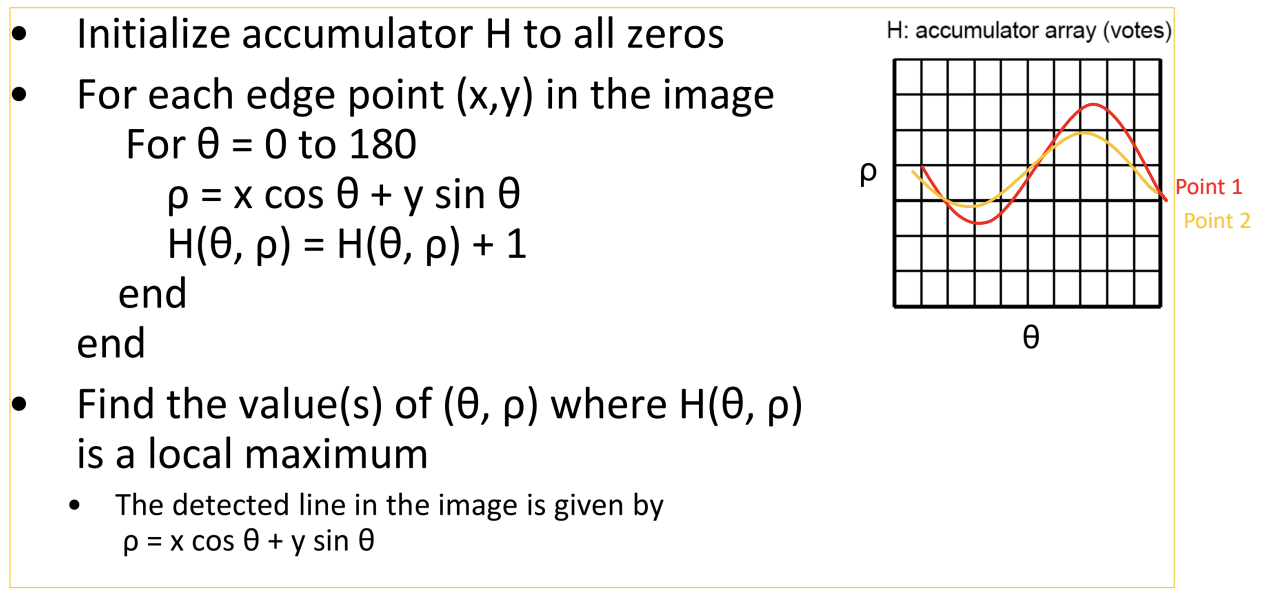
Deal with Noise
**噪声影响:**当我们有一些随机数据点时候,霍夫变换也会形成一条虚假的直线,因为总有那么几条曲线会相交。
如何处理噪声:
1. 选择合适的网格大小 (Choose a good grid)
这是霍夫变换中最纠结的参数(离散化程度)。
- 太粗糙 (Too coarse): 如果格子(Bin)划得太大,很多本不共线的点会被强行归到一个格子里,导致“假高票”。
- 太精细 (Too fine): 如果格子划得太小,由于像素本身有误差,原本属于同一条直线的点,可能会投到相邻的几个不同格子里。结果票数被分散了,导致找不到明显的峰值(漏检)。
- 结论: 这是一个权衡(Trade-off),需要根据图像分辨率和容错率仔细调整。
2. 给邻居投票 / 平滑处理 (Increment neighboring bins)
为了解决上面提到的“网格太细导致票数分散”的问题,我们引入**“软标签 (Soft label)”**机制。
- 做法: 当一个点计算出参数 $ (\theta, \rho) $ 时,不光给这一个格子加分,也给它周围的邻居格子加分(比如中心加1分,旁边加0.5分)。
- 好处: 相当于对参数空间做了一次平滑 (Smoothing)。这样即使有测量误差,票数也能汇聚在一起,形成一个比较宽但很结实的峰值。
3. 过滤无关特征 (Get rid of irrelevant features)
这是为了解决上一张 PPT 提到的“随机噪点也能凑出假直线”的问题。
- 做法: 不要让图像上所有的点都来投票。
- 筛选: 只选取那些梯度幅值(Gradient Magnitude)很大的点。
- 逻辑: 梯度大意味着这里是强边缘(轮廓清晰),不太可能是噪点。只让“可信度高”的点参与投票,能极大减少参数空间里的噪声背景。
incorporate image gradient
霍夫变换结合图像梯度
我们不再需要从 0-180度计算每一条直线了,因为这些处在边缘上的点,他们的边缘方向正好和梯度方向垂直,即 $ \theta $就是梯度方向,因此我们的算法变为了如下:
for each edge point $ (x,y) $:
$ \theta $= gradient orientation at $ (x,y) $
$ \rho = x \cos \theta + y \sin \theta $
$ H(\theta , \rho) += 1 $
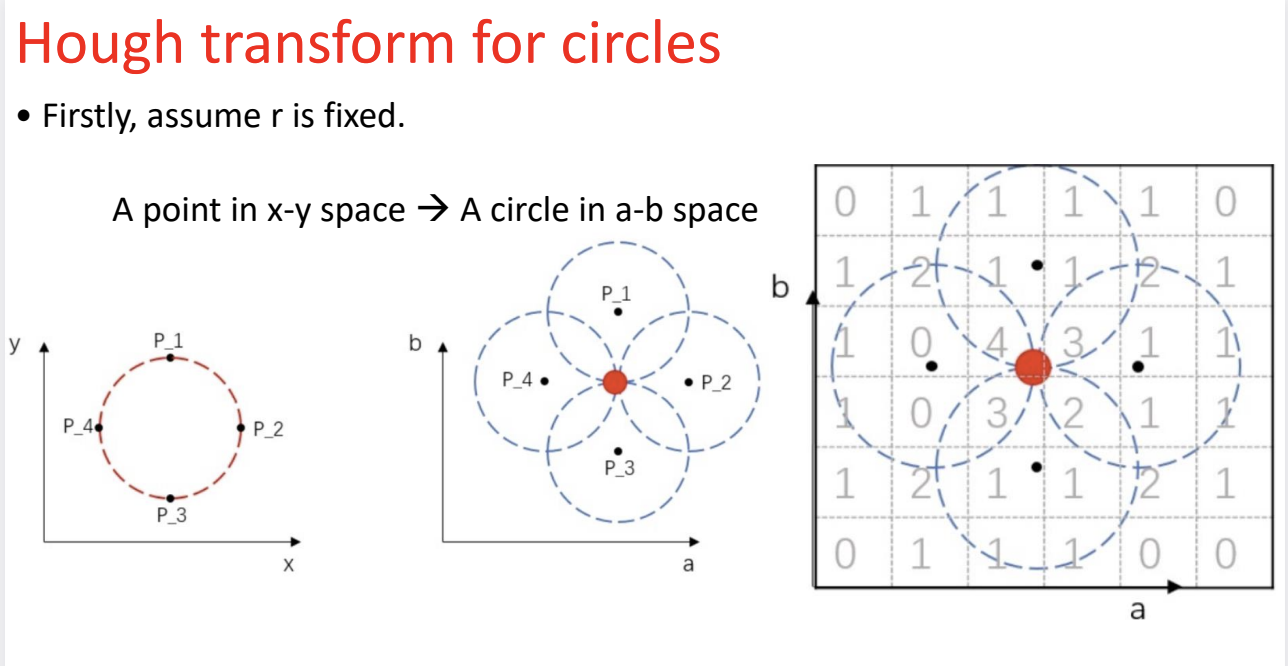
Hough transform for circles
圆的霍夫变换
我们首先假设原始圆的半径是已知的,(因为我们有圆心坐标 $ (a,b) $和 半径$ r $,如果都不知道则需要一个三维的参数空间,这样会导致计算量爆炸)
Generalized Hough transform
广义的霍夫变换
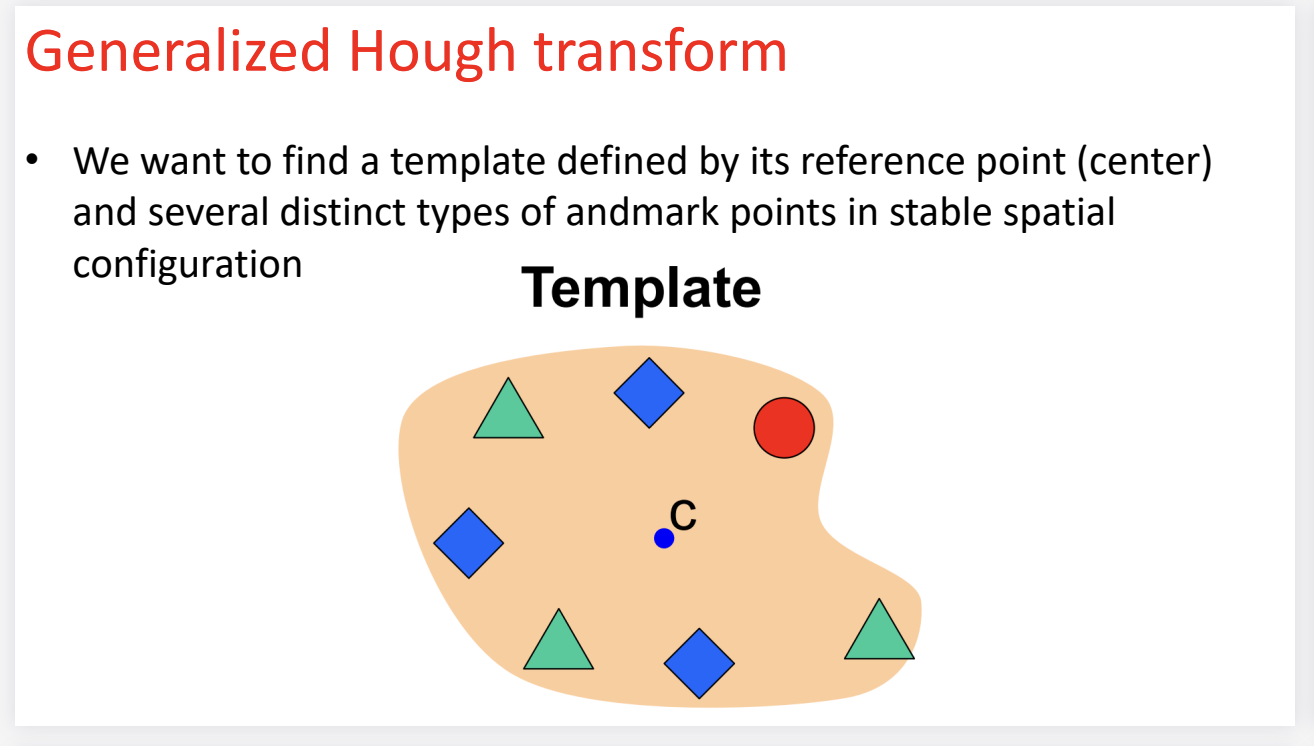
第一张图:定义问题 (The Template)
- 目标: 我们想在一个新图像中找到这个不规则的橙色形状。
- 核心思想: 虽然这个形状没有公式,但它有固定的特征分布。
- 我们可以选定一个参考点 (Reference Point / Center),比如图中的蓝点 C。
- 这个形状是由若干个特征点 (Landmarks) 组成的(比如绿色的三角形、蓝色的菱形、红色的圆形)。
- 关键约束: 无论这个物体移动到哪里,“绿三角形”和“中心点C”之间的相对位置(距离和方向)是永远不变的。
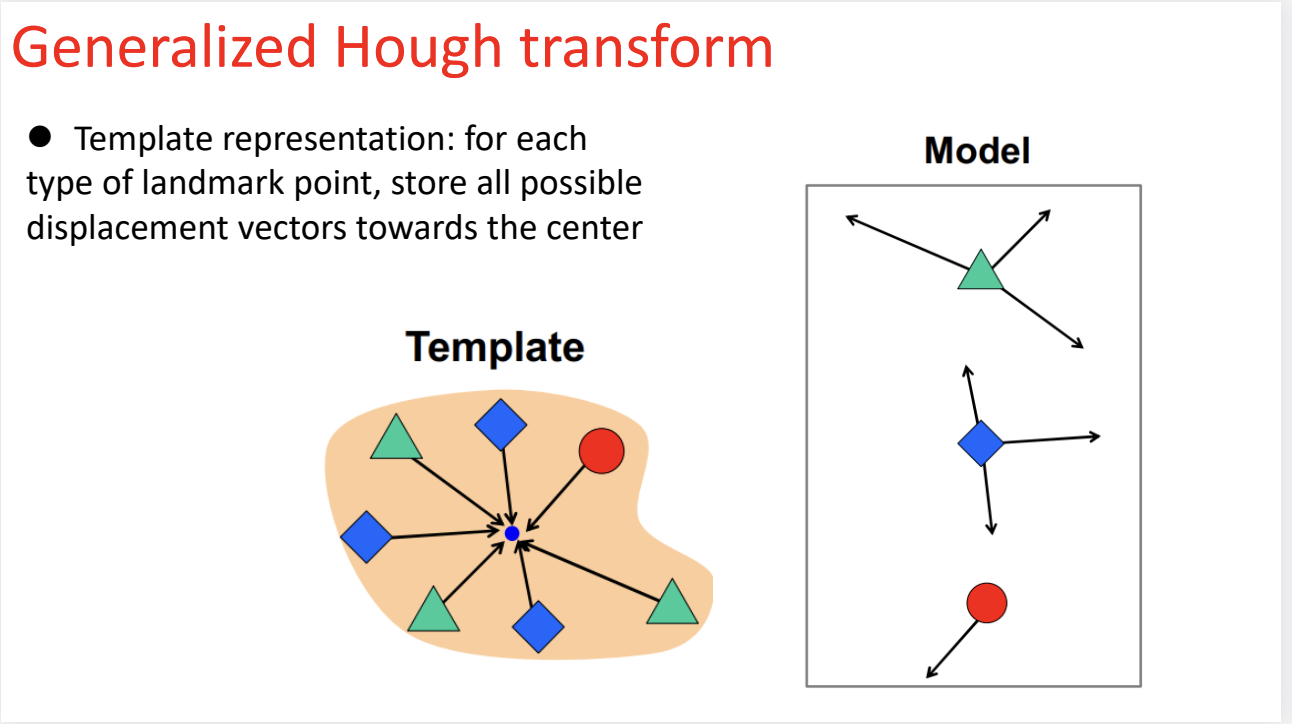
第二张图:建立模型 / 训练阶段 (Model Building)
这是算法的学习过程。我们需要建立一个查找表 (Look-up Table),告诉计算机每个特征点和中心的关系。
- 左图(模板):
- 这是我们已知的标准模板。
- 算法测量每一个特征点到中心点 $ C $ 的位移向量 (Displacement Vector)。
- 比如:从“绿三角形”出发,向右下角走 5 厘米就是中心。
- 右图(模型/查找表):
- 这是计算机存储下来的知识库。
- 重要细节: 请看右边的模型框里的绿三角形,它对应了两个箭头。
- 为什么有两个? 因为在左边的模板里,其实有两个绿三角形。当你只看到一个“绿三角形”时,你并不知道它是上面的那个还是下面的那个。所以,为了保险起见,计算机把这两个可能的位移向量都存了下来。
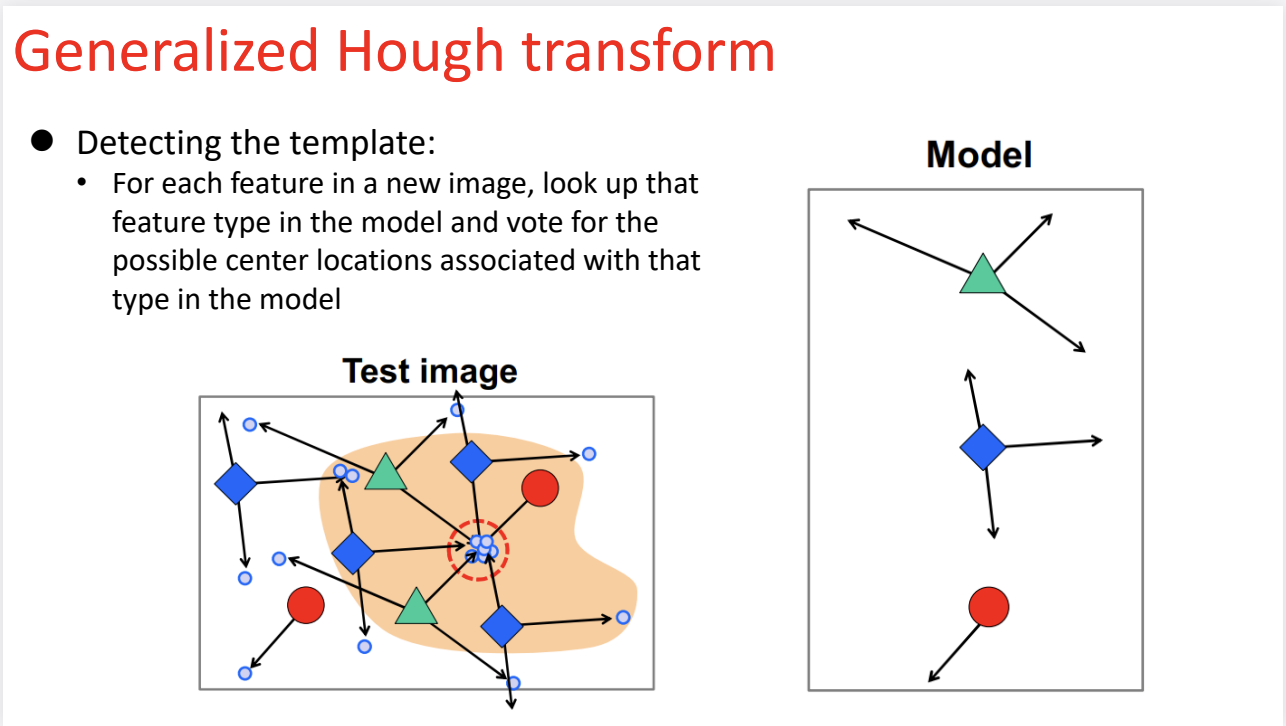
第三张图:检测阶段 / 投票 (Detecting / Voting)
这是算法在新图像(Test Image) 中工作的过程。
- 场景: 测试图像里有一堆乱七八糟的东西(蓝色小圆圈是噪声),还有我们被部分遮挡的目标物体。
- 流程:
- 发现特征: 算法在图像中扫描,比如它发现了一个“绿三角形”。
- 查表: 它去查上一张图建立的“模型”。模型告诉它:“只要看到了绿三角形,中心点可能在方向 A,也可能在方向 B”。
- 投票: 于是,这个绿三角形就向这两个可能的位置分别投出一票(画出箭头)。
- 集体行动: 接着,图像里检测到的蓝菱形、红圆圈也都纷纷根据模型查表、投票。
- 结果 (Result):
- 你可以看到图中那个红色的虚线圆圈区域。
- 虽然每个点都在瞎猜(投多个方向),但所有属于该物体的特征点,都会不约而同地把票投向同一个位置——真正的中心点 C。
- 而背景里的噪声(那些孤立的蓝色小点),它们的投票是杂乱无章的,无法形成聚类。
- 最终,票数最高的那个点,就是检测到的物体中心。
总结
广义霍夫变换的本质就是**“凭特征找中心”**:
- 以前(圆检测): “我是个边缘点,我知道圆心距离我 $ R $ 这么远,我画个圈投票。”
- 现在(广义 GHT): “我是个‘绿三角形’,我知道根据经验,中心点通常在我的右下角 5 厘米处,所以我往那里投一票。”
这种方法非常强大,因为它不依赖数学公式,只要你有模板,你可以检测任意形状的物体。
Pros vs. Cons
这张表总结了霍夫变换作为一个独立算法的自身特性。
| 分类 | 核心要点 (中文) | 详细解释 |
|---|---|---|
| 优点 (Pros) | 1. 抗遮挡与非局部性 | 即使物体被遮挡(断开了),或者边缘点在图像上相距很远,只要它们在参数空间投到同一个点,算法依然能把它们连起来。 |
| 2. 多实例检测 | 这是它最强的地方。它可以在一次运行中同时检测出多条直线或多个圆,不需要像 RANSAC 那样一次只拟合一个。 | |
| 3. 对噪声有一定鲁棒性 | 因为噪声点通常是随机分布的,它们很难在参数空间的某一个格子里形成一致的”高票数”,因此会被自然过滤。 | |
| 缺点 (Cons) | 1. 维度灾难(复杂度指数爆炸) | 直线只有 2 个参数 $(\theta, \rho)$ 还可以;圆有 3 个参数 $(a,b,r)$ 勉强能算;如果是椭圆(5 个参数),计算量和内存消耗会呈指数级增长,无法接受。 |
| 2. 虚假峰值 (Spurious peaks) | 也就是之前提到的,如果背景噪声太多,它们纯靠运气可能会在某个格子里凑出高分,导致算法误检出不存在的形状。 | |
| 3. 网格大小难选 | 也就是”Grid size”问题。网格太大精度低,网格太小票数分散,很难找到一个完美的平衡点。 |
| 比较维度 | 霍夫变换 (Hough Transform) | RANSAC (随机采样一致性) |
|---|---|---|
| 适用场景 | 专门用于检测几何形状(直线、圆、椭圆等)。 | 非常通用,适用于各种数学模型(包括非几何的,如矩阵变换、物体识别)。 |
| 核心优势 (Pros) | 1. 能处理多目标:擅长处理多个形状重叠或交叉的情况。 2. 抗遮挡:对部分遮挡非常鲁棒。 3. 直接参数估计:直接算出形状参数。 |
1. 抗离群点:在包含大量干扰数据(Outliers)时非常强。 2. 自适应:算法灵活,可根据数据情况调整。 3. 模型无关:不局限于几何图形。 |
| 核心劣势 (Cons) | 1. 计算昂贵:内存和时间消耗大。 2. 参数敏感:非常依赖网格划分和投票阈值的设定。 3. 局限性:难以处理非标准或极其复杂的形状。 |
1. 需要调参:迭代次数、采样数、距离阈值都需要调。 2. 极端情况失效:如果垃圾数据比例极高(Extremely high),可能怎么抽都抽不到好样本。 3. 随机性:结果精度依赖于采样的运气(通常需后接最小二乘法微调)。 |
| 一句话总结 | “全图投票法”:适合找好几个几何图形,不怕遮挡,但怕参数多。 | “随机试错法”:适合从垃圾堆里找出一个最佳模型,精度高,但怕离群点多到离谱。 |