1. 原始优化问题
一切始于我们要解决的标准优化问题。我们称之为原始问题 (Primal Problem)。
标准形式:
$$
\begin{aligned}
\min_{x} \quad & f_0(x) \
\text{s.t.} \quad & f_i(x) \le 0, \quad i = 1, \dots, m \
h_i(x) = 0, \quad i = 1, \dots, p
\end{aligned}
$$
- $x \in \mathbb{R}^n$:优化变量。
- $f_0(x)$:目标函数。
- $f_i(x)$:不等式约束。
- $h_i(x)$:等式约束。
- $p^*$:原始问题的最优值(Optimal Value)。
2. 拉格朗日函数
为了解决带约束的问题,我们的核心思想是将“硬约束”转化为目标函数中的“软惩罚”。我们要构造一个包含所有约束的新函数。
定义:
拉格朗日函数 $L: \mathbb{R}^n \times \mathbb{R}^m \times \mathbb{R}^p \to \mathbb{R}$ 定义为:
$$ L(x, \lambda, \nu) = f_0(x) + \sum_{i=1}^m \lambda_i f_i(x) + \sum_{i=1}^p \nu_i h_i(x) $$
- $\lambda_i$:对应不等式约束的拉格朗日乘子(Dual Variable),要求 $\lambda_i \ge 0$。
- $\nu_i$:对应等式约束的拉格朗日乘子,符号没有限制。
直观理解:
拉格朗日函数就是把原本不能违背的规则(约束),变成了违背就要付出代价(价格 $\lambda, \nu$)的经济学模型。
3. 原始问题的另一种视角
让我们观察一下这个量:$\sup_{\lambda \succeq 0, \nu} L(x, \lambda, \nu)$ (即固定 $x$,调整 $\lambda, \nu$ 让 $L$ 最大)。
- 情况 A:$x$ 违反了约束
- 如果某个 $f_i(x) > 0$,我们可以取 $\lambda_i \to +\infty$,使得 $L \to +\infty$。
- 如果某个 $h_i(x) \neq 0$,我们可以取 $\nu_i \to \infty$(同号),使得 $L \to +\infty$。
- 情况 B:$x$ 满足所有约束(可行)
- 此时 $f_i(x) \le 0$,为了最大化 $L$,由于 $\lambda_i \ge 0$,最优策略是取 $\lambda_i=0$(或者如果 $f_i(x)=0$,$\lambda_i$ 取任意值不影响)。
- $h_i(x) = 0$,这一项直接消失。
- 结果:$L = f_0(x)$。
结论:
$$ \sup_{\lambda \succeq 0, \nu} L(x, \lambda, \nu) = \begin{cases} f_0(x) & \text{若 } x \text{ 可行} \ +\infty & \text{若 } x \text{ 不可行} \end{cases} $$
因此,原始问题完全等价于:
$$ p^* = \min_x \left( \sup_{\lambda \succeq 0, \nu} L(x, \lambda, \nu) \right) $$
(先让对手把惩罚加到最大,然后我再选择 $x$ 让痛苦最小)。
4. 拉格朗日对偶函数
现在我们交换 $\min$ 和 $\sup$ 的顺序,这就引出了对偶世界的核心。
定义:
对偶函数 $g(\lambda, \nu)$ 定义为 $L$ 关于 $x$ 的下确界:
$$ g(\lambda, \nu) = \inf_x L(x, \lambda, \nu) = \inf_x \left( f_0(x) + \sum \lambda_i f_i(x) + \sum \nu_i h_i(x) \right) $$
关键性质:
凹性 (Concavity):无论原函数 $f_0, f_i$ 是否是凸函数,对偶函数 $g(\lambda, \nu)$ 永远是凹函数(因为它是关于 $\lambda, \nu$ 的仿射函数的逐点下确界)。这是对偶理论最美妙的地方。
下界性质 (Lower Bound Property):
对任意 $\lambda \ge 0$ 和任意 $\nu$,都有:
$$ g(\lambda, \nu) \le p^* $$证明思路:
对于任意可行解 $\tilde{x}$,有 $f_i(\tilde{x}) \le 0$ 且 $h_i(\tilde{x}) = 0$。
$$ \sum \lambda_i f_i(\tilde{x}) + \sum \nu_i h_i(\tilde{x}) \le 0 $$
所以 $L(\tilde{x}, \lambda, \nu) \le f_0(\tilde{x})$。
而 $g(\lambda, \nu)$ 是 $L$ 关于 $x$ 的最小值,肯定比 $L(\tilde{x}, \dots)$ 更小。
即 $g(\lambda, \nu) \le f_0(\tilde{x})$。这对所有可行 $\tilde{x}$ 成立,自然对最优的 $p^*$ 也成立。
5. 拉格朗日对偶问题
既然 $g(\lambda, \nu)$ 是 $p^$ 的下界,我们希望能找到*最好的(最大的)下界。
对偶问题定义:
$$
\begin{aligned}
\max_{\lambda, \nu} \quad & g(\lambda, \nu) \
\text{s.t.} \quad & \lambda \ge 0
\end{aligned}
$$
设最优对偶值为 $d^*$。
几何解释:
- 原始问题是找山谷的最低点(Min)。
- 对偶问题是在山谷下面顶天花板,试图让天花板尽可能高(Max),但不能超过最低点。
6. 强对偶与弱对偶
我们已经知道 $d^* \le p^*$。
弱对偶性 (Weak Duality):
$$ d^* \le p^* $$
这个性质永远成立。差值 $p^* - d^*$ 称为对偶间隙 (Duality Gap)。强对偶性 (Strong Duality):
$$ d^* = p^* $$
如果成立,意味着对偶间隙为 0。我们可以通过求解容易的对偶问题(它是凸优化),直接得到原始问题的最优值。Slater 条件 (Slater’s Condition):
什么时候强对偶成立?
如果原始问题是凸优化问题($f_0, f_i$ 是凸函数,$h_i$ 是仿射函数),且满足 Slater 条件,则强对偶成立。
Slater 条件内容: 存在一个点 $x$,使得所有不等式约束严格成立($f_i(x) < 0$)。这叫“严格可行点”。
7. KKT 条件
KKT 条件是连接原始解 ($x^*$) 和对偶解 ($\lambda^*, \nu^*$) 的桥梁。
重要地位:
- 对于一般的优化问题(非凸),KKT 是最优解的必要条件(如果 $x^*$ 是最优解,它必须满足 KKT)。
- 对于凸优化问题(且满足 Slater 条件),KKT 是最优解的充要条件。
KKT 四大天王:
假设 $f_0, f_i, h_i$ 均可微。$x^*, \lambda^*, \nu^*$ 是最优解的充要条件如下:
平稳性条件 (Stationarity): 拉格朗日函数的梯度为 0。
$$ \nabla_x L(x^*, \lambda^*, \nu^*) = \nabla f_0(x^*) + \sum \lambda_i^* \nabla f_i(x^*) + \sum \nu_i^* \nabla h_i(x^*) = 0 $$
(物理意义:力系平衡。目标函数的下降力被约束的推力抵消)原始可行性 (Primal Feasibility): $x^*$ 必须满足原问题约束。
$$ f_i(x^*) \le 0, \quad h_i(x^*) = 0 $$对偶可行性 (Dual Feasibility): 乘子必须非负。
$$ \lambda_i^* \ge 0 $$互补松弛条件 (Complementary Slackness): (最核心的条件)
$$ \lambda_i^* f_i(x^*) = 0, \quad \forall i $$解释:
- 如果 $f_i(x^*) < 0$(约束未激活,点在内部),则必须有 $\lambda_i^* = 0$(该约束不起作用,不产生力)。
- 如果 $\lambda_i^* > 0$(约束产生推力),则必须有 $f_i(x^*) = 0$(点紧贴在边界上)。
- 这就像“注水”,只有碰到了墙壁(边界),墙壁才会给你反作用力。
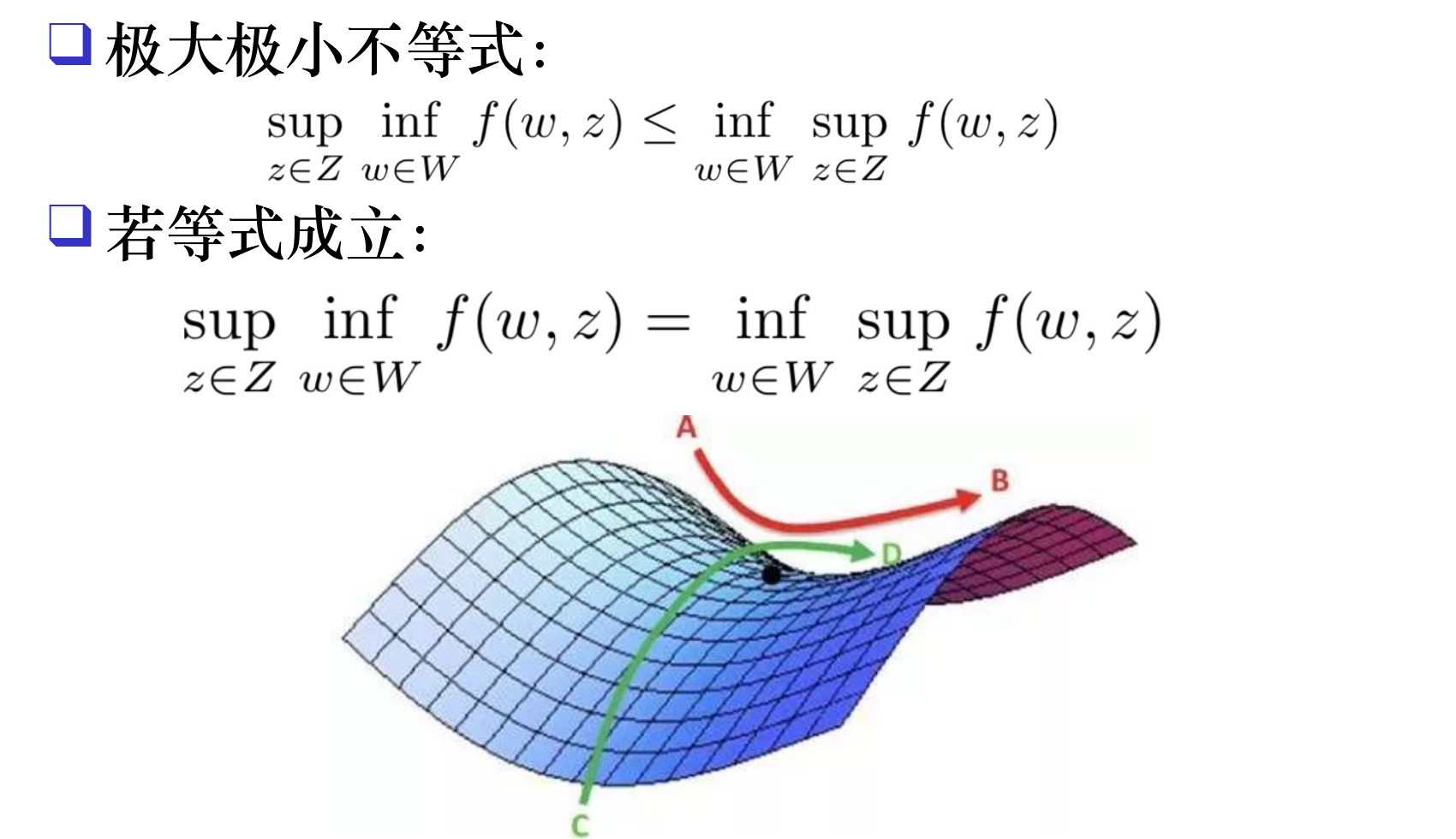
8. 鞍点解释
我们可以用鞍点 (Saddle Point) 的概念来总结。
考虑函数 $L(x, \lambda, \nu)$:
- 对于 $x$,我们在找极小值(谷底)。
- 对于 $\lambda, \nu$,我们在找极大值(山峰)。
如果强对偶性成立,最优解 $(x^*, \lambda^*, \nu^*)$ 就是拉格朗日函数的鞍点:
$$ L(x^*, \lambda, \nu) \le L(x^*, \lambda^*, \nu^*) \le L(x, \lambda^*, \nu^*) $$
- 右边不等式:固定最优的 $\lambda^*, \nu^*$,$x^*$ 使得 $L$ 最小(平稳性条件)。
- 左边不等式:固定最优的 $x^*$,$\lambda^*, \nu^*$ 使得 $L$ 最大(对应原始可行性和互补松弛)。